题目内容
19.画出函数y=-2x+1(x>0)的图象(1)计算并填写表中的空格
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 5 | 3 | 1 | -1 | -3 | … |
(3)用平滑的曲线连接这些点.
分析 (1)自变量分别取-2,-1,0,1,2代入解析式求出函数值即可.
(2)x作为横坐标,y作为纵坐标,写出坐标即可.
(3)利用描点法画出图象即可.
解答 解:(1)填表如下:
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 5 | 3 | 1 | -1 | -3 | … |
5,3,1,-1,-3.
(2)根据表中的数值在平面直角系中描点,坐标为(-2,5),(-1,3),( 0,1),( 1,-2),( 2,-3)
故答案分别为(-2,5),(-1,3),(0,1),(1,-2),(2,-3).
(3)图象如图所示:
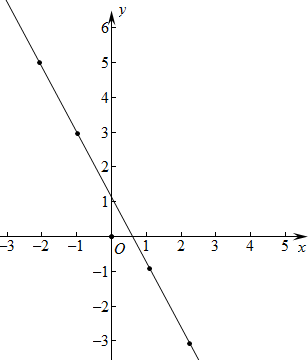
点评 本题考查一次函数的图象,解题的关键是掌握画函数图象的步骤①列表②描点③连线,连线时从左到右用光滑的曲线连接,属于基础题,中考常考题型.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
7.下列计算结果正确的是( )
| A. | a3+a3=a6 | B. | x2•x3=x6 | C. | (-a)2÷2a=2a | D. | (-2xy2)3=-8x3y6 |
4. 如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则下列说法不正确的是( )
如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则下列说法不正确的是( )
 如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则下列说法不正确的是( )
如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则下列说法不正确的是( )| A. | 方程ax2+bx+c=0的两根为x1=-1,x2=2 | |
| B. | 抛物线y=ax2+bx+c与直线y=2x+4无交点 | |
| C. | 当y>0时,-1<x<2 | |
| D. | 当y>2时,$\frac{1}{2}$<x<1 |
8.下列计算正确的是( )
| A. | $(-\frac{1}{2})^{2}=-\frac{1}{4}$ | B. | 3a-2=$\frac{1}{3{a}^{2}}$ | C. | (-1)0=1 | D. | 00=1 |
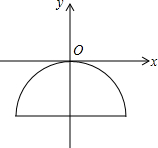 如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.
如图,一抛物线型石拱桥在如图所示的直角坐标系中,桥的最大高度是16米,跨度是46米.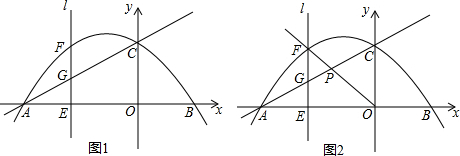
 如图,在平面直角坐标系中,Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为$\frac{3\sqrt{3}}{4}$.
如图,在平面直角坐标系中,Rt△AOB的直角边OA、OB分别在x轴、y轴正半轴上,OA=1,∠OBA=30°,将△AOB绕点A顺时针旋转,使AB的对应边AD恰好落在x轴上,点O的对应点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为$\frac{3\sqrt{3}}{4}$.