题目内容
12.已知抛物线y=ax2+bx+c从经过三点:A(0,1),B(1,3),C(-1,1),确定a,b,c的值,并画出这条抛物线.分析 把点A、B、C的坐标代入函数解析式得到关于a、b、c的三元一次方程组,然后求解即可;再求出抛物线上另一点坐标和顶点坐标,然后作出大致函数图象.
解答 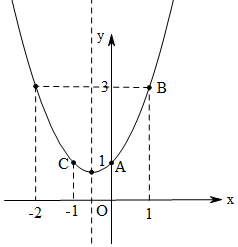 解:将A(0,1),B(1,3),C(-1,1)代入二次函数解析式得:
解:将A(0,1),B(1,3),C(-1,1)代入二次函数解析式得:
$\left\{\begin{array}{l}{c=1}\\{a+b+c=3}\\{a-b+c=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=1}\\{c=1}\end{array}\right.$,
则抛物线解析式为:y=x2+x+1;
∵y=x2+x+1=(x+$\frac{1}{2}$)2+$\frac{3}{4}$;
所以,顶点坐标为(-$\frac{1}{2}$,$\frac{3}{4}$),
由对称性得:抛物线还过(-2,3),
画函数图象如图所示.
点评 此题考查了待定系数法求二次函数解析式,二次函数图象的画法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
17.下列分式中,属于最简分式的是( )
| A. | $\frac{6}{3x}$ | B. | $\frac{4x}{{x}^{2}+3x}$ | C. | $\frac{x+2}{{x}^{2}+4}$ | D. | $\frac{3-x}{x-3}$ |
4.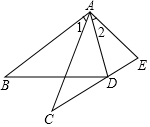 如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )
如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )
 如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )
如图,要使△ABD和△ACE全等,已知条件AB=AC,∠1=∠2,不能添加的条件是( )| A. | BD=CE | B. | AD=AE | C. | ∠B=∠C | D. | ∠ADB=∠AEC |
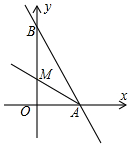 如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴交于A,B两点,∠BAO的平分线所在的直线AM的解析式是y=-$\frac{1}{2}$x+3.
如图,直线y=-$\frac{4}{3}$x+8与x轴、y轴交于A,B两点,∠BAO的平分线所在的直线AM的解析式是y=-$\frac{1}{2}$x+3.