题目内容
2.在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图1和图2,请根据相关信息,解答下列问题;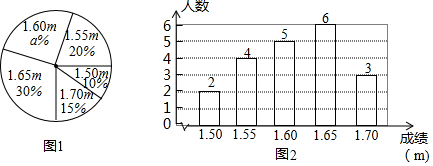
(1)图一中成绩为1.60m的部分所占百分比为25%;
(2)统计的这组初赛成绩的众数为1.65,中位数为1.60;
(3)根据这组初赛成绩,由高到低确定9人进入复赛,请问初赛成绩为1.65m的运动员能否进入复赛,不必说明理由.
分析 (1)用整体1减去其它所占的百分比,即可求出a的值;
(2)根据众数和中位数的定义,分别进行解答即可;
(3)根据中位数的意义可直接判断出能否进入复赛.
解答 解:(1)根据题意得:a%=1-20%-10%-15%-30%=25%;
故答案为:25%;
(2)观察条形统计图得:在这组数据中,1.65出现了6次,出现的次数最多,
∴这组数据的众数是1.65;
将这组数据从小到大排列,其中处于中间的两个数都是1.60,
则这组数据的中位数是1.60.
故答案为:1.65,1.60;
(3)初赛成绩为1.65m的运动员能进入复赛.
理由:共有20个人,中位数是第10、11个数的平均数,根据中位数可以判断出能否进入前9名,
∵1.65m>1.60m,
∴能进入复赛.
点评 本题考查了条形统计图与扇形统计图,众数、中位数的定义.解题时注意:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.

练习册系列答案
相关题目
7.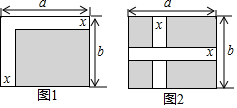 通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
 通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )
通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是( )| A. | a(b-x)=ab-ax | B. | b(a-x)=ab-bx | ||
| C. | (a-x)(b-x)=ab-ax-bx | D. | (a-x)(b-x)=ab-ax-bx+x2 |
14.若一个直角三角形的三边长为3、4、x,则x的值是( )
| A. | 5 | B. | 5或$\sqrt{6}$ | C. | $\sqrt{5}$ | D. | 5或$\sqrt{7}$ |
11.甲、乙、丙三地海拔高度分别为-100米、-300米、500米,那么最高的地方比最低的地方高( )
| A. | 400米 | B. | 600米 | C. | 200米 | D. | 800米 |
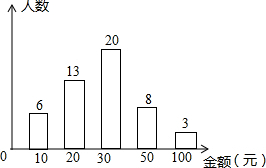 随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.
随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.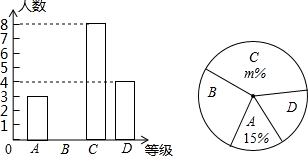
 如图是由 4 个边长为 1 的正方的平行四边形的个数是形构成的网格.用没有刻度的直尺在这个网格中最多可以作出一组对边长度为 $\sqrt{5}$的平行四边形的个数是( )
如图是由 4 个边长为 1 的正方的平行四边形的个数是形构成的网格.用没有刻度的直尺在这个网格中最多可以作出一组对边长度为 $\sqrt{5}$的平行四边形的个数是( )