题目内容
20．若点P（x，y）在第一象限内，且点P到两坐标轴的距离相等，并满足2x-y=4，则$\left\{\begin{array}{l}{x=}&{\;}\\{y=}&{\;}\end{array}\right.$44．
分析 根据点到两坐标轴的距离相等，可得方程，根据解方程组，可得答案．
解答 解：由题意，得
$\left\{\begin{array}{l}{y=x}\\{2x-y=4}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$．
故答案为：4，4．
点评 本题考查了点的坐标，利用点的坐标相等得出方程组是解题关键．
练习册系列答案
相关题目
11．-2100×0.5100×（-1）2013-$\frac{1}{2}$计算结果是（ ）
| A． | -1 | B． | 1 | C． | $\frac{1}{2}$ | D． | 0 |
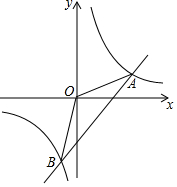如图，在平面直角坐标系中，不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A（m，3），B（-2，n），其中m＞0，n＜0
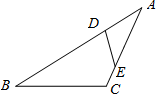如图，△ABC中，点D，E分别在边AB，AC上，∠AED=∠B，若AD=2，AE=3，CE=1，则BD的长为（ ）
5．下列各数中，最小的数是（ ）
| A． | -3 | B． | -$\frac{1}{2}$ | C． | 2 | D． | 0 |
9．下面的四个图形中，能够通过基本图形平移得到的图形有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
