Question

17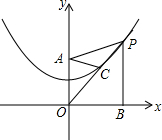．如图，点P是抛物线y=$\frac{1}{4}$x²+1上在第一象限内的点，线段PO交抛物线于点C，PB⊥x轴于点B，点A的坐标是（0，2），当点C是OP的中点时，下列说法错误的是（　　）

• A． PA=PB
• B． ∠POB=45°
• C． PA=2AC
• D． PB=3

Answer 1

分析 设点P（x，$\frac{1}{4}$x²+1），由C为OP中点可得点C坐标为（$\frac{x}{2}$，$\frac{1}{8}$x²+$\frac{1}{2}$），将点C坐标代入抛物线解析式求得x的值，即可知点P、C的坐标，根据PB⊥x轴于点B知PB、OB的长，由点A坐标（0，2）根据两点间距离公式计算AC、PA的长度，再逐一判断各选项即可．

解答 解：∵点P是抛物线y=$\frac{1}{4}$x²+1上在第一象限内的点，
∴设点P坐标为（x，$\frac{1}{4}$x²+1），
∵点C是OP的中点，
∴点C坐标为（$\frac{x}{2}$，$\frac{1}{8}$x²+$\frac{1}{2}$），
∵点C在抛物线y=$\frac{1}{4}$x²+1上，
∴$\frac{1}{4}$（$\frac{x}{2}$）²+1=$\frac{1}{8}$x²+$\frac{1}{2}$，
解得：x=2$\sqrt{2}$或x=-2$\sqrt{2}$（舍），
∴点P的坐标为（2$\sqrt{2}$，3），点C的坐标为（$\sqrt{2}$，$\frac{3}{2}$），
A、由PB⊥x轴于点B知PB=3，
由A（0，2）得PA=$\sqrt{（0-2\sqrt{2}）^{2}+（2-3）^{2}}$=3，
∴PA=PB；故A选项正确；

B、在RT△POB中，∵PB=3，OB=2$\sqrt{2}$，
∴PB≠OB，
∴∠POB≠45°，故B选项错误；

C、由A（0，2）、C（$\sqrt{2}$，$\frac{3}{2}$）知AC=$\sqrt{（\sqrt{2}-0）^{2}+（\frac{3}{2}-2）^{2}}$=$\frac{3}{2}$，
∵PA=3，
∴PA=2AC，故C选项正确；

D、由点P（2$\sqrt{2}$，3）且PB⊥x轴于点B知PB=3，故D选项正确；
故选：B．

点评 本题主要考查二次函数的图象与性质及两点间距离的计算，根据点P及OP中点C均在抛物线上求得抛物线解析式是解题的关键