题目内容
14.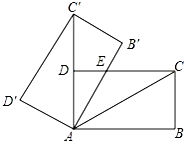 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )| A. | 12 | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
分析 根据旋转后AC的中点恰好与D点重合,利用旋转的性质得到直角三角形ACD中,∠ACD=30°,再由旋转后矩形与已知矩形全等及矩形的性质得到∠DAE为30°,进而得到∠EAC=∠ECA,利用等角对等边得到AE=CE,设AE=CE=x,表示出AD与DE,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出EC的长,即可求出三角形AEC面积.
解答 解:∵旋转后AC的中点恰好与D点重合,即AD=$\frac{1}{2}$AC′=$\frac{1}{2}$AC,
∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,
∴∠DAD′=60°,
∴∠DAE=30°,
∴∠EAC=∠ACD=30°,
∴AE=CE,
在Rt△ADE中,设AE=EC=x,则有DE=DC-EC=AB-EC=6-x,AD=$\frac{\sqrt{3}}{3}$×6=2$\sqrt{3}$,
根据勾股定理得:x2=(6-x)2+(2$\sqrt{3}$)2,
解得:x=4,
∴EC=4,
则S△AEC=$\frac{1}{2}$EC•AD=4$\sqrt{3}$.
故选:B.
点评 此题考查了旋转的性质,含30度直角三角形的性质,勾股定理,以及等腰三角形的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列说法中,正确的是( )
| A. | 如果a2=b2,那么a=b | B. | 如果ac=bc,那么a=b | ||
| C. | 如果a=b,那么2a+c=b+2c | D. | 如果a-c=b-c,那么a=b |
2.数据0.00000026用科学记数法表示为2.6×10n,则n的值是( )
| A. | 6 | B. | 7 | C. | -6 | D. | -7 |
19.不等式2x-2<0的解集是( )
| A. | x<1 | B. | x<-1 | C. | x>1 | D. | x>-1 |
4.目前节能灯在城市已基本普及,今年云南省面向县级及农村地区推广,为相应号召,某商场计划用3800元购进节能灯120只,这两种节能灯的进价、售价如下表:
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)全部售完120只节能灯后,该商场获利润多少元?
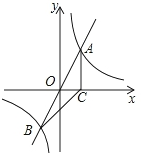 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.