题目内容
17. 如图,平行四边形ABCD中,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.
如图,平行四边形ABCD中,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.(1)求证:△ABE≌△CDF;
(2)当四边形ABCD满足什么条件时,四边形AECF是菱形?证明你的结论.
分析 (1)由平行四边形的性质可得AB=CD,∠ABE=∠CDF,再因为MA⊥AN,NC⊥BC可得∠BAM=∠DCN,利用ASA定理可证得结论;
(2)利用菱形的性质可得AC⊥EF,由全等三角形的性质可得AE=CF,由平行四边形的判定定理可得四边形AECF为平行四边形,利用菱形的判定定理得出结论.
解答 (1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,∠BAD=∠BCD,
∵MA⊥AN,NC⊥BC,
∴∠BAM=∠DCN,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{AB=CD}\\{∠BAM=∠DCN}\end{array}\right.$,
∴△ABE≌△CDF(ASA);
(2)解:四边形ABCD是菱形时,四边形AECF是菱形.
∵△ABE≌△CDF,
∴AE=CF,
∵MA⊥AN,NC⊥BC,
∴AM∥CN,
∴四边形AECF为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥EF,
∴四边形AECF为菱形.
点评 本题主要考查了平行四边形的性质和菱形的性质及判定定理,综合运用各定理是解答此题的关键.

练习册系列答案
相关题目
8.正六边形的边心距为$\sqrt{3}$,则该正六边形的外接圆半径为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{3}$ |
12.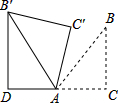 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=3$\sqrt{2}$,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=3$\sqrt{2}$,则AD的长为( )
 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=3$\sqrt{2}$,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点A逆时针旋转75°得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=3$\sqrt{2}$,则AD的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
9.“微信发红包”是刚刚兴起的一种娱乐方式,为了解所在单位员工春节期间使用微信发红包的情况,小红随机调查了15名同事,结果如表:
则此次调查中平均每个红包的钱数的众数为2元,中位数为5元.
| 平均每个红包的钱数(元) | 2 | 5 | 10 | 20 | 50 |
| 人数 | 7 | 4 | 2 | 1 | 1 |
