题目内容
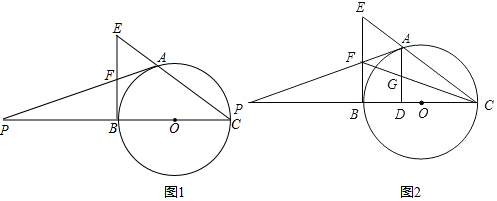
14. 如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )| A. | $\frac{18}{5}$ | B. | $\frac{16}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{4}{5}$ |
分析 根据翻折变换的性质得到BE=FE,∠BEA=∠FEA,根据三角形外角的性质得到∠BEA+∠FEA=∠EFC+∠ECF,得到∠BEA=∠ECF,根据平行线的性质得到CF⊥BF,根据勾股定理即可得到结论.
解答  解:连接BF,
解:连接BF,
∵BC=AD=6,点E是BC的中点,
∴EC=BE=3,
由翻折变换的性质可知,BE=FE,∠BEA=∠FEA,
∴EF=EC,
∴∠EFC=∠ECF,
∵∠BEA+∠FEA=∠EFC+∠ECF,
∴∠BEA=∠BCF,
∴AE∥CF,
∵AE⊥BF,
∴CF⊥BF,
∵AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=5,
∴BG=$\frac{AB•BE}{AE}$=$\frac{12}{5}$,
∴BF=2BG=$\frac{24}{5}$,
∴CF=$\sqrt{B{C}^{2}-B{F}^{2}}$=$\frac{18}{5}$.
故选A.
点评 本题考查的是翻折变换的性质和锐角三角函数的定义,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
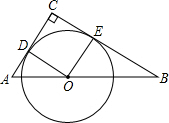 如图,在△ABC中,∠C=90°,点O是斜边AB上一点,以O为圆心的⊙O分别与边AC、BC相切于点D、E,连接OD、OE.
如图,在△ABC中,∠C=90°,点O是斜边AB上一点,以O为圆心的⊙O分别与边AC、BC相切于点D、E,连接OD、OE.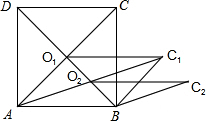 如图,正方形ABCD的面积为2$\sqrt{5}$cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为$\frac{\sqrt{5}}{{2}^{5}}$cm2.
如图,正方形ABCD的面积为2$\sqrt{5}$cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为$\frac{\sqrt{5}}{{2}^{5}}$cm2.