题目内容
2.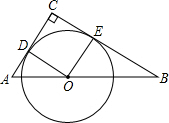 如图,在△ABC中,∠C=90°,点O是斜边AB上一点,以O为圆心的⊙O分别与边AC、BC相切于点D、E,连接OD、OE.
如图,在△ABC中,∠C=90°,点O是斜边AB上一点,以O为圆心的⊙O分别与边AC、BC相切于点D、E,连接OD、OE.(1)求证:四边形CDOE是正方形;
(2)若AC=3,BC=4,求⊙O的半径.
分析 (1)先证明四边形ODCE为矩形,再根据OD=OE,可得出四边形CDOE为正方形;
(2)连接OC,先设圆O的半径为r,利用面积法,列出方程即可解决问题;
解答 (1)证明:∵AC、BC分别为半圆O的切线,
∴∠ODC=∠OEC=90°,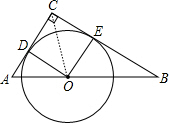
∵∠C=90°,
∴四边形ODCE为矩形,
∵OD=OE,
∴四边形CDOE为正方形;
(2)解:连接OC,设⊙O的半径为r.
∵S△ACB=S△ACO+S△BCO,
∴$\frac{1}{2}$×3×4=$\frac{1}{2}$•3•r+$\frac{1}{2}$•4•r,
∴r=$\frac{12}{7}$.
点评 本题考查了切线的性质以及正方形的判定,切线垂直于过切点的半径,三个角为直角且有一组邻边相等的四边形为正方形,解题的关键是学会利用面积法,构建方程解决问题,属于中考常考题型..

练习册系列答案
相关题目
7. 如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
 如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )| A. | 75° | B. | 85° | C. | 140° | D. | 145° |
14. 如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
 如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )| A. | $\frac{18}{5}$ | B. | $\frac{16}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{4}{5}$ |
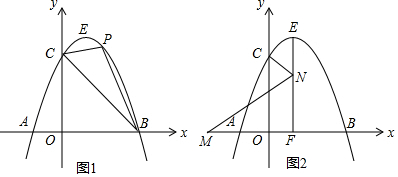
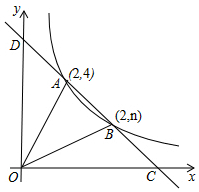 如图,直线y=ax+b与反比例函数$y=\frac{m}{x}$(x>0)的图象交于A(2,4),B(4,n)两点,与x轴,y轴分别交于C,D两点.
如图,直线y=ax+b与反比例函数$y=\frac{m}{x}$(x>0)的图象交于A(2,4),B(4,n)两点,与x轴,y轴分别交于C,D两点. 如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.
如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.