题目内容
19.解不等式组$\left\{\begin{array}{l}6-2x>2x-6\\ 2x+1>\frac{3+x}{2}\end{array}\right.$,并写出它的整数解.分析 先求出每个不等式的解集,再求出不等式组的解集,即可得出答案.
解答 解:$\left\{\begin{array}{l}{6-2x>2x-6①}\\{2x+1>\frac{3+x}{2}②}\end{array}\right.$
∵由①得:x<3,
由②得:x$>\frac{1}{3}$,
∴不等式组的解集为:$\frac{1}{3}<x<3$,
∴不等式组的整数解为:1,2.
点评 本题考查了解一元一次不等式和解一元一次不等式组、不等式组的整数解等知识点,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
7. 如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
 如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )| A. | 75° | B. | 85° | C. | 140° | D. | 145° |
14. 如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
 如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )| A. | $\frac{18}{5}$ | B. | $\frac{16}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{4}{5}$ |
 如图,△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是76°.
如图,△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是76°. 如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.
如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.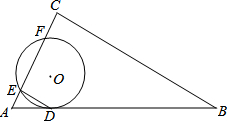 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.