题目内容
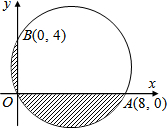 如图,一圆过O、A、B三点,已知斜线部分面积为aπ+b,其中a,b为有理数,则a-b=
如图,一圆过O、A、B三点,已知斜线部分面积为aπ+b,其中a,b为有理数,则a-b=考点:勾股定理,坐标与图形性质
专题:
分析:连接AB,由点A、B的坐标得到OA、OB的长,再利用勾股定理列式求出AB,然后根据阴影部分的面积等于半圆的面积减去Rt△AOB的面积列式计算即可得解.
解答: 解:如图,连接AB,
解:如图,连接AB,
∵A(8,0),B(0,4),
∴OA=8,OB=4,
由勾股定理得,AB=
=
=4
,
∴圆的半径为2
,
S阴影=
π(2
)2-
×4×8,
=10π-16,
∵斜线部分面积为aπ+b,其中a,b为有理数,
∴a=10,b=-16,
∴a-b=10-(-16)=26.
故答案为:26.
 解:如图,连接AB,
解:如图,连接AB,∵A(8,0),B(0,4),
∴OA=8,OB=4,
由勾股定理得,AB=
| OA2+OB2 |
| 82+42 |
| 5 |
∴圆的半径为2
| 5 |
S阴影=
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
=10π-16,
∵斜线部分面积为aπ+b,其中a,b为有理数,
∴a=10,b=-16,
∴a-b=10-(-16)=26.
故答案为:26.
点评:本题考查了勾股定理,坐标与图形性质,阴影部分的面积,作辅助线构造出直角三角形和半圆并表示出阴影部分的面积是解题的关键.

练习册系列答案
相关题目
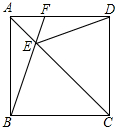 如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
