题目内容
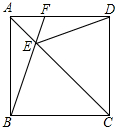 如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.(1)问:EB与ED有何关系?请说明理由;
(2)延长BE交AD于F,当∠BED=120°时,求∠EFD的度数.
考点:正方形的性质
专题:
分析:(1)根据正方形的四条边都相等可得AB=AD,对角线平分一组对角线可得∠BAC=∠DAC=45°,然后利用“边角边”证明△ABE和△ADE全等,再根据全等三角形对应边相等证明即可;
(2)根据全等三角形对应角相等可得∠AEB=∠AED,再根据等角的补角相等可得∠BEC=∠DEC=60°,根据对顶角相等可得∠AEF=∠BEC,再根据平角的定义列式计算即可得解.
(2)根据全等三角形对应角相等可得∠AEB=∠AED,再根据等角的补角相等可得∠BEC=∠DEC=60°,根据对顶角相等可得∠AEF=∠BEC,再根据平角的定义列式计算即可得解.
解答:解:(1)EB=ED.
理由如下:在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴EB=ED;
(2)∵△ABE≌△ADE,
∴∠AEB=∠AED,
∴∠BEC=∠DEC,
∵∠BED=120°,
∴∠BEC=∠DEC=60°,
∵∠AEF=∠BEC=60°(对顶角相等),
∠EAD=45°
∴∠EFD=60°+45°=105°.
理由如下:在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
在△ABE和△ADE中,
|
∴△ABE≌△ADE(SAS),
∴EB=ED;
(2)∵△ABE≌△ADE,

∴∠AEB=∠AED,
∴∠BEC=∠DEC,
∵∠BED=120°,
∴∠BEC=∠DEC=60°,
∵∠AEF=∠BEC=60°(对顶角相等),
∠EAD=45°
∴∠EFD=60°+45°=105°.
点评:本题考查了正方形的性质,全等三角形的判定与性质,对顶角相等的性质,熟记各性质并判断出全等三角形是解题的关键.

练习册系列答案
相关题目
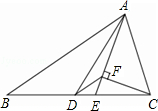 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,求DF的长.
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,求DF的长.
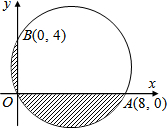 如图,一圆过O、A、B三点,已知斜线部分面积为aπ+b,其中a,b为有理数,则a-b=
如图,一圆过O、A、B三点,已知斜线部分面积为aπ+b,其中a,b为有理数,则a-b=