题目内容
(
)2004•(
)2003= ．已知x+
=5，那么x2+
= ．
| 5 |
| 3 |
| 3 |
| 5 |
| 1 |
| x |
| 1 |
| x2 |
考点：幂的乘方与积的乘方,同底数幂的乘法,完全平方公式
专题：
分析：先化为同底数幂的乘法，然后进行运算即可；等式两边分别进行平方，即可求解．
解答：解：原式=（
）2004（
）-2003=
；
等式两边同时平方得：（x+
）2=25，
即x2+
+2=25，
则x2+
=23．
故答案为：
，23．
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
等式两边同时平方得：（x+
| 1 |
| x |
即x2+
| 1 |
| x2 |
则x2+
| 1 |
| x2 |
故答案为：
| 5 |
| 3 |
点评：本题考查了积的乘方和幂的乘方以及同底数幂的乘法、完全平方公式，掌握各知识点的运算法则是解答本题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
如图，矩形ABCD中，AB=6，BC=10，将矩形沿AC折叠，使点B与点E重合，AD与EC相交于点F．
如图，矩形OABC是一把粉刷墙壁用的刷子，其中OA=3，OC=4，若一工人在一次粉刷时仅把矩形刷子靠在墙上绕点O旋转90°，则墙壁该次被粉刷的面积是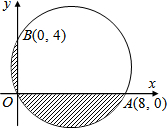
如图，一圆过O、A、B三点，已知斜线部分面积为aπ+b，其中a，b为有理数，则a-b=