题目内容
矩形一个角的平分线分矩形一边成2cm和3cm，则这个矩形的面积为 ．
考点：矩形的性质
专题：
分析：根据AD∥BC，理解平行线的性质，以及角平分线的定义，即可证得∠ABE=∠AEB，利用等边对等角可以证得AB=AE，然后分AE=2cm，DE=3cm和AE=3cm，DE=2cm两种情况即可求得矩形的边长，从而求解．
解答：
解：∵AD∥BC，
∴∠AEB=∠EBC
又∵BE平分∠ABC，即∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AB=AE．
当AE=2cm，DE=3cm时，AD=BC=5cm，AB=CD=AE=2cm．
∴矩形ABCD的面积是：2×5=10cm2；
当AE=3cm，DE=2cm时，AD=BC=5cm，AB=CD=AE=3cm，
∴矩形ABCD的周长是：5×3=15cm2．
故矩形的周长是：10cm2或15cm2．
故答案是：10cm2或15cm2．
解：∵AD∥BC，∴∠AEB=∠EBC
又∵BE平分∠ABC，即∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AB=AE．
当AE=2cm，DE=3cm时，AD=BC=5cm，AB=CD=AE=2cm．
∴矩形ABCD的面积是：2×5=10cm2；
当AE=3cm，DE=2cm时，AD=BC=5cm，AB=CD=AE=3cm，
∴矩形ABCD的周长是：5×3=15cm2．
故矩形的周长是：10cm2或15cm2．
故答案是：10cm2或15cm2．
点评：此题考查了矩形的性质以及等腰三角形的判定与性质．此题难度适中，注意掌握数形结合思想与分类讨论思想的应用．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
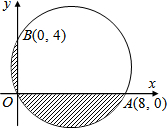如图，一圆过O、A、B三点，已知斜线部分面积为aπ+b，其中a，b为有理数，则a-b=
如图，AB是⊙O的弦，OC⊥AB于点D，交⊙O于点C，若⊙O的半径为10，CD=4，那么AB的长为