题目内容
在△ABC中,BD、CE相交于点F,试在下列设定的条件中选择若干个条件作为题设,另一个条件作为结论,组合成一个真命题,并写出证明.
①∠A=α;
②BD、CE分别是∠ABC、∠ACB的平分线;
③BD、CE是△ABC的两条高;
④∠BFC=90°+
α;
⑤∠BFC=180°-α.
①∠A=α;
②BD、CE分别是∠ABC、∠ACB的平分线;
③BD、CE是△ABC的两条高;
④∠BFC=90°+
| 1 |
| 2 |
⑤∠BFC=180°-α.
考点:命题与定理,三角形内角和定理,三角形的外角性质
专题:证明题
分析:由①③为条件,⑤为结论组成一个命题,先根据垂直的定义得到∠ADB=90°,∠AEC=90°,再根据四边形内角和定义计算出∠DFE,然后利用对顶角的性质求解.
解答: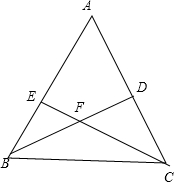 已知:∠A=α,BD、CE是△ABC的两条高,如图,
已知:∠A=α,BD、CE是△ABC的两条高,如图,
求证:∠BFC=180°-α.
证明:∵BD、CE是△ABC的两条高,
∴∠ADB=90°,∠AEC=90°,
∴∠DFE=360°-∠ADF-∠AEF-∠A=180°-α,
∵∠BFC=∠DFE,
∴∠BFC=180°-α.
 已知:∠A=α,BD、CE是△ABC的两条高,如图,
已知:∠A=α,BD、CE是△ABC的两条高,如图,求证:∠BFC=180°-α.
证明:∵BD、CE是△ABC的两条高,
∴∠ADB=90°,∠AEC=90°,
∴∠DFE=360°-∠ADF-∠AEF-∠A=180°-α,
∵∠BFC=∠DFE,
∴∠BFC=180°-α.
点评:本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
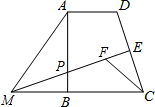 已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E是CD的中点,过点E作CD的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.
已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E是CD的中点,过点E作CD的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA. 如图,矩形ABCD中,AB=6,BC=10,将矩形沿AC折叠,使点B与点E重合,AD与EC相交于点F.
如图,矩形ABCD中,AB=6,BC=10,将矩形沿AC折叠,使点B与点E重合,AD与EC相交于点F.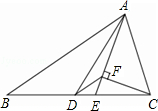 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,求DF的长.
如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,求DF的长.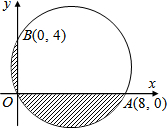 如图,一圆过O、A、B三点,已知斜线部分面积为aπ+b,其中a,b为有理数,则a-b=
如图,一圆过O、A、B三点,已知斜线部分面积为aπ+b,其中a,b为有理数,则a-b=