Question

2．直线y=-$\frac{1}{2}$x+2与x轴，y轴分别交于A，B两点，在y轴上有点C（0，4），动点M从点A以每秒1个单位长度的速度沿x轴向左移动．
（1）求△COM的面积S与M的移动时间t之间的函数关系式；
（2）当t为何值时，△ABM是等腰三角形，并求此时点M的坐标．

Answer 1

分析 （1）考虑点M在原点右边或左边两种情形即可．
（2）分三种情形讨论，①当AM₁=BM₁时，求出直线AB的垂直平分线HM₁为y=2x-3，即可解决问题，②AB=AM₂时，③当BA=BM₃时根据等腰三角形定义即可解决．

解答 解：（1）如图1中，当0＜t≤4时，s=$\frac{1}{2}$•OM•CO=2（4-t）=-2t+8，
当t＞4时，s=$\frac{1}{2}$•OM′•CO=2（t-4）=2t-8，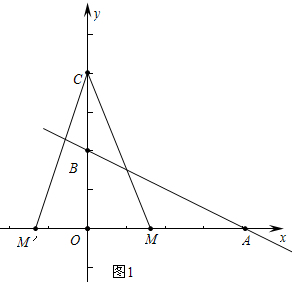

（2）如图2中，①当AM₁=BM₁时，直线AB的垂直平分线HM₁为y=2x-3，所以点M₁坐标为（$\frac{3}{2}$，0）．
②AB=AM₂时，点M₂（4-2$\sqrt{5}$，0）．
③当BA=BM₃时，点M₃（-4，0）．
综上所述点M坐标为（$\frac{3}{2}$，0）或（-4，0）或（4-2$\sqrt{5}$，0）．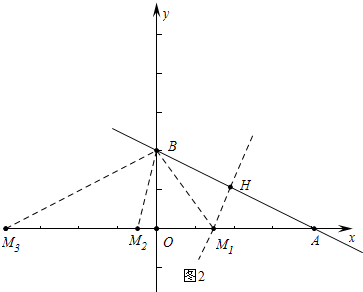

点评 本题考查一次函数的有关知识、勾股定理、等腰三角形的定义等知识，学会分类讨论的思想，容易漏解，解题的关键是正确画出图形，属于中考常考题型．