题目内容
18．
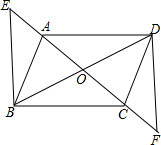如图，四边形ABCD对角线交于点O，且O为AC中点，AE=CF，DF∥BE，求证：四边形ABCD是平行四边形．
分析 由已知条件和平行线的性质得出OE=OF，∠E=∠F，由ASA证明△BOE≌△DOF，得出对应边相等OB=OD，即可证出四边形ABCD是平行四边形．
解答 证明：∵O为AC中点，
∴OA=OC，
∵AE=CF，
∴OE=OF，
∵DF∥BE，
∴∠E=∠F，
在△BOE和△DOF中，$\left\{\begin{array}{l}{∠E=∠F}&{\;}\\{OE=OF}&{\;}\\{∠BOE=∠DOF}&{\;}\end{array}\right.$，
∴△BOE和△DOF（ASA），
∴OB=OD，
又∵OA=OC，
∴四边形ABCD是平行四边形．
点评 本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的性质；熟练掌握平行四边形的判定方法，证明三角形全等得出对应边相等是解决问题的关键．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
如图所示，∠ABC与∠ACB的内角平分线交于点O，∠ABC的内角平分线与∠ACB的外角平分线交于点D，∠ABC与∠ACB的相邻外角平分线交于点E，且∠A=60°，则∠BOC=120°，∠D=30°，∠E=60°．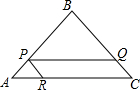
已知：如图，Rt△ABC中，∠B=90°，AB=BC=8cm，P为AB上任意一点，PR∥BC，PQ∥AC，S?PQCR=16cm2，求AP的长．
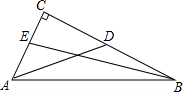如图，在△ABC中，∠C=90°，AD，BE是中线，BE=2$\sqrt{10}$，AD=5，求AB的长（提示：设CE=x，CD=y）．
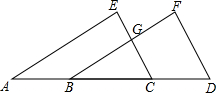如图，已知：如图，EC∥FD，∠F=∠E，点A，B，C，D在一条直线上，EA与FB有怎样的位置关系？为什么？
李大叔带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示．结合图形解答下列问题