题目内容
16．若（x+4）（x-5）=x2+mx+n，则m+n=（ ）| A． | 21 | B． | -21 | C． | 19 | D． | -19 |
分析 根据因式分解与整式的乘法互为逆运算，把（x+4）（x-5）利用乘法公式展开，即可求出m，n的值．
解答 解：∵（x+4）（x-5）=x2-x-20，
又∵多项式x2+mx+n可以分解为（x+4）（x-5），
∴m=-1，n=-20；
∴m+n=-21．
故选B．
点评 此题考查了因式分解的意义，关键是根据因式分解与整式的乘法互为逆运算解答．
练习册系列答案
相关题目
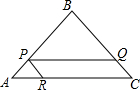已知：如图，Rt△ABC中，∠B=90°，AB=BC=8cm，P为AB上任意一点，PR∥BC，PQ∥AC，S?PQCR=16cm2，求AP的长．
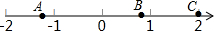如图，一只蚂蚁从点A沿数轴向右直爬2个单位到达点B，再直爬向C点停止，已知点A表示-$\sqrt{2}$，点C表示2，设点B所表示的数为m．