题目内容
5.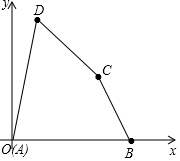 如图,已知在平面直角坐标系中,四边形各顶点的坐标分别为A(0,0),B(9,0),C(7,4),D(2,8),求四边形ABCD的面积.
如图,已知在平面直角坐标系中,四边形各顶点的坐标分别为A(0,0),B(9,0),C(7,4),D(2,8),求四边形ABCD的面积.
分析 利用分割法,把四边形分割成两个三角形加上一个梯形后再求面积.
解答  解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
S=S△OED+SEFCD+S△CFB
=$\frac{1}{2}$×AE×DE+$\frac{1}{2}$×(CF+DE)×EF+$\frac{1}{2}$×FC×FB.
=$\frac{1}{2}$×2×8+$\frac{1}{2}$×(8+4)×5+$\frac{1}{2}$×2×4=42.
故四边形ABCD的面积为42平方单位.
点评 此题主要考查了点的坐标的意义以及与图形相结合的具体运用.要掌握两点间的距离公式和图形有机结合起来的解题方法.

练习册系列答案
相关题目
15.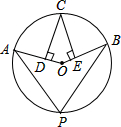 如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
 如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )
如图,OA,OB分别为⊙O的半径,若CD⊥OA,CE⊥OB,垂足分别为D,E,∠P=70°,则∠DCE的度数为( )| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
14. 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
 如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
如图,已知点E(-4,2),F(-2,-2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )| A. | (2,-1)或(-2,1) | B. | (8,-4)或(-8,-4) | C. | (2,-1) | D. | (8,-4) |
15.已知反比例函数y=$\frac{k-1}{x}$的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )
| A. | 方程有两个不想等的实数根 | B. | 方程不一定有实数根 | ||
| C. | 方程有两个相等的实数根 | D. | 方程没有实数根 |
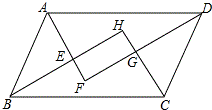 如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.
如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形. 如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.
如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.