题目内容
15.已知反比例函数y=$\frac{k-1}{x}$的图象位于第二、第四象限,那么关于x的一元二次方程x2+2x+k=0的根的情况是( )| A. | 方程有两个不想等的实数根 | B. | 方程不一定有实数根 | ||
| C. | 方程有两个相等的实数根 | D. | 方程没有实数根 |
分析 首先根据反比例函数的性质求得k的取值范围,从而利用根的判别式确定方程的根的情况即可.
解答 解:∵反比例函数y=$\frac{k-1}{x}$的图象位于第二、第四象限,
∴k-1<0,
解得:k<1,
∴关于x的一元二次方程x2+2x+k=0中△=4-4k>0,
∴方程有两个不相等的实数根,
故选A.
点评 本题考查了反比例函数的性质及根的判别式的知识,解题的关键是能够根据反比例函数的性质确定k的取值范围,难度不大.

练习册系列答案
相关题目
3.2-1的相反数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
10. 如图所示,直线a、b被直线c所截,∠1与∠2是( )
如图所示,直线a、b被直线c所截,∠1与∠2是( )
 如图所示,直线a、b被直线c所截,∠1与∠2是( )
如图所示,直线a、b被直线c所截,∠1与∠2是( )| A. | 内错角 | B. | 同位角 | C. | 同旁内角 | D. | 邻补角 |
7. 如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
 如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
4.若|2016-a|+$\sqrt{a-2017}$=a,则a-20162的值是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
5.一元二次方程x2+2x+2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 只有一个实数根 |
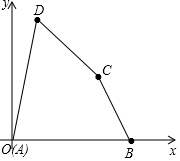 如图,已知在平面直角坐标系中,四边形各顶点的坐标分别为A(0,0),B(9,0),C(7,4),D(2,8),求四边形ABCD的面积.
如图,已知在平面直角坐标系中,四边形各顶点的坐标分别为A(0,0),B(9,0),C(7,4),D(2,8),求四边形ABCD的面积.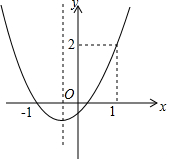 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论: