题目内容
12.(1)先化简再求值:$\frac{x+1}{y}$÷$\frac{{{x^2}-1}}{y^2}$,其中:x=3,y=5.(2)已知:$\sqrt{x-4}$+$\sqrt{2x+y}$=0,求x-y的值.
分析 (1)先把分式的除法转化为乘法即可化简,然后将x=3,y=5代入化简后的式子即可解答本题;
(2)根据$\sqrt{x-4}$+$\sqrt{2x+y}$=0,可以求得x、y的值,从而可以求得x-y的值.
解答 解:(1)$\frac{x+1}{y}$÷$\frac{{{x^2}-1}}{y^2}$
=$\frac{x+1}{y}×\frac{{y}^{2}}{(x+1)(x-1)}$
=$\frac{y}{x-1}$,
当x=3,y=5时,
原式=$\frac{5}{3-1}=\frac{5}{2}$;
(2)∵$\sqrt{x-4}$+$\sqrt{2x+y}$=0,
∴$\left\{\begin{array}{l}{x-4=0}\\{2x+y=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=4}\\{y=-8}\end{array}\right.$,
∴x-y=4-(-8)=12.
点评 本题考查分式的化简求值、非负数的性质,解题的关键是明确分式化简求值的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列说法错误的是( )
| A. | 三角形中至少有两个锐角 | |
| B. | 两条边及一角对应相等的三角形全等 | |
| C. | 两个角及一边对应相等的三角形全等 | |
| D. | 三角形的外角大于不相邻的内角 |
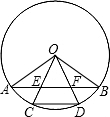 如图,OA、OB是⊙O的两条半径,且OA⊥OB,C、D是$\widehat{AB}$的三等两点,OC、OD分别交AB于E、F,则AE、CD与BF相等吗?为什么?
如图,OA、OB是⊙O的两条半径,且OA⊥OB,C、D是$\widehat{AB}$的三等两点,OC、OD分别交AB于E、F,则AE、CD与BF相等吗?为什么? 如图,化简:|a|-|a+b|+|c-a|+|b+c|
如图,化简:|a|-|a+b|+|c-a|+|b+c|