题目内容
5.解关于x的方程x+$\frac{ab}{x}$=a+b的根为:x=a或x=b,如①x+$\frac{2}{x}$=3的根为x=1或x=2;②x+$\frac{6}{x}$=5的根为x=2或x=3,求关于x的方程x+$\frac{{n}^{2}+n}{x-3}$=2n+4(n为正整数)的根,你的答案是:n+3或n+4.分析 根据题意得出结合x+$\frac{ab}{x}$=a+b的根为:x=a或x=b,进而得出答案.
解答 解:由题意可得:x+$\frac{{n}^{2}+n}{x-3}$=2n+4可变形为:x-3+$\frac{n(n+1)}{x-3}$=2n+4-3,
则x-3+$\frac{n(n+1)}{x-3}$=n+n+1,
故x-3=n或n+1,
则x=n+3或n+4.
故答案为:n+3或n+4.
点评 此题主要考查了分式方程的解,正确得出分式方程与解的关系是解题关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
20.已知菱形的两条对角线长分别为6和8,则该菱形的对称中心到任意一边的距离为( )
| A. | 10 | B. | 5 | C. | 2.5 | D. | 2.4 |
15.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. | 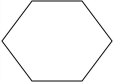 | C. | 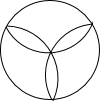 | D. | 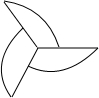 |
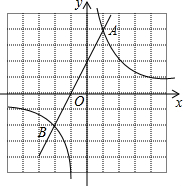 如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).
如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).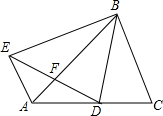 在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.
在△ABC中,BD是∠ABC的平分线,在△ABC外取一点E,使得∠EAB=∠ACB,AE=DC,并且线段ED与AB交于点F.求证:EF=DF.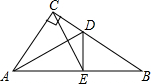 如图,已知在△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB,若∠DCE=∠DEC,已知CD=$\frac{3}{2}$,BC=4
如图,已知在△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB,若∠DCE=∠DEC,已知CD=$\frac{3}{2}$,BC=4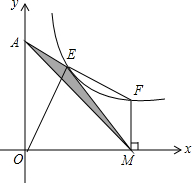 如图,E,F在双曲线y=$\frac{8}{x}$上,FE交y轴于点A,AE=EF,FM⊥x轴于M,求S△AME.
如图,E,F在双曲线y=$\frac{8}{x}$上,FE交y轴于点A,AE=EF,FM⊥x轴于M,求S△AME.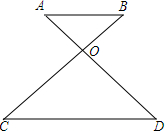 如图,OA:OD=OB:OC=1:2,OB=3.
如图,OA:OD=OB:OC=1:2,OB=3.