题目内容
3.已知(-1,y1),(0.5,y2),(1.7,y3)是直线y=-9x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是( )| A. | y3>y2>y1 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
分析 由y=-9x+b(b为常数)可知k=-9<0,故y随x的增大而减小,由-1<0.5<1.7,可得y1,y2,y3的大小关系.
解答 解:∵k=-9<0,
∴y随x的增大而减小,
∵-1<0.5<1.7,
∵y1>y2>y3,
故选:B.
点评 本题主要考查一次函数的增减性,熟练掌握一次函数的增减性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知△ABC≌△DEF,∠A=78°,∠B=35°,则∠F=( )
| A. | 78° | B. | 35° | C. | 77° | D. | 67° |
14.已知P1(-1,y1),P(-2,y2)是一次函数y=$\frac{1}{3}$x-1的图象上的两点,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 以上都不对 |
11.若干人做某项工作,每个人的工作效率相同,m个人做n天可完成,如果增加a人,则完成这项工作所需天数为( )
| A. | n-a | B. | $\frac{mn}{m+a}$ | C. | $\frac{mn}{m-a}$ | D. | n+a |
18.在Rt△ABC中,∠C=90°,∠A的对边为a,∠B的对边为b,且满足a2-ab-b2=0,则tanA=( )
| A. | 1 | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\frac{1-\sqrt{5}}{2}$ | D. | $\frac{1±\sqrt{5}}{2}$ |
8.下列命题中是假命题的是( )
| A. | 等腰三角形一边上的中线和高互相重合 | |
| B. | 等腰三角形的底角一定是锐角 | |
| C. | 有一条边相等的两个等边三角形全等 | |
| D. | 顶角相等,底边上的高也相等的两个等腰三角形全等 |
 如图,AB∥CD,AC、BC相交于点E,∠B=52°,求∠C.
如图,AB∥CD,AC、BC相交于点E,∠B=52°,求∠C.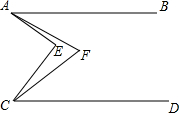 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=∠$\frac{3}{4}$AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=∠$\frac{3}{4}$AEC.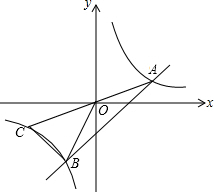 如图,直线y=x+b与双曲线y=$\frac{k}{x}$交于A、B两点,延长AO交双曲线于C点,连接BC,且AB=2BC=4$\sqrt{2}$,则k=3.
如图,直线y=x+b与双曲线y=$\frac{k}{x}$交于A、B两点,延长AO交双曲线于C点,连接BC,且AB=2BC=4$\sqrt{2}$,则k=3.