题目内容
12.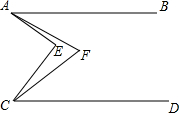 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=∠$\frac{3}{4}$AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=∠$\frac{3}{4}$AEC.
分析 连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=180°-(4x°+4y°),求出∠AEC=4(x°+y°),∠AFC═3(x°+y°),即可得出答案.
解答 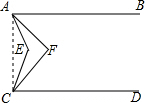 证明:连接AC,
证明:连接AC,
设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+4x°+∠ACE+4y°=180°,
∴∠CAE+∠ACE=180°-(4x°+4y°),∠FAC+∠FCA=180°-(3x°+3y°)
∴∠AEC=180°-(∠CAE+∠ACE)
=180°-[180°-(4x°+4y°)]
=4x°+4y°
=4(x°+y°),
∠AFC=180°-(∠FAC+∠FCA)
=180°-[180°-(3x°+3y°)]
=3x°+3y°
=3(x°+y°),
∴∠AFC=$\frac{3}{4}$∠AEC.
点评 本题考查了平行线性质和三角形内角和定理的应用,解题时注意:两直线平行,同旁内角互补.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
2.下列计算正确的是( )
| A. | 2$\sqrt{2}$×3$\sqrt{3}$=6$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | 2$\sqrt{3}$-$\sqrt{3}$=2 | D. | 2÷$\sqrt{2}$=$\sqrt{2}$ |
3.已知(-1,y1),(0.5,y2),(1.7,y3)是直线y=-9x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是( )
| A. | y3>y2>y1 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
17.若a的倒数是它本身,b的平方根等于它本身,那么(a2+b)2的值是( )
| A. | 1 | B. | 8 | C. | ±1 | D. | ±8 |
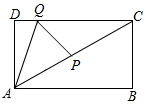 如图,长方形ABCD中,AD=a,DC=b,(a,b为常数),∠CAB=30°,点P是对角线AC的中点,点Q是线段CD上的动点,则AQ+QP的最小值为$\sqrt{3}a$.
如图,长方形ABCD中,AD=a,DC=b,(a,b为常数),∠CAB=30°,点P是对角线AC的中点,点Q是线段CD上的动点,则AQ+QP的最小值为$\sqrt{3}a$.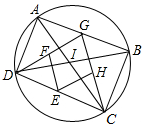 如图,AC与BD是⊙I的直径,AD=4,CD=10,点G是AB上一动点,点E、F、H分别是DC、DG、CG的中点.
如图,AC与BD是⊙I的直径,AD=4,CD=10,点G是AB上一动点,点E、F、H分别是DC、DG、CG的中点. 如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为$\sqrt{3}$.
如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为$\sqrt{3}$.