下列命题中是假命题的是( )A．等腰三角形一边上的中线和高互相重合B．等腰三角形的底角一定是锐角C．有一条边相等的两个等边三角形全等D．顶角相等.底边上的高也相等的两个等腰三角形全等题目和参考答案——青夏教育精英家教网—

题目内容

8．下列命题中是假命题的是（　　）

	A．	等腰三角形一边上的中线和高互相重合
	B．	等腰三角形的底角一定是锐角
	C．	有一条边相等的两个等边三角形全等
	D．	顶角相等，底边上的高也相等的两个等腰三角形全等

分析利用等腰三角形的性质及等腰三角形的判定方法分别判断后即可确定正确的选项．

解答解：A、等腰三角形底边上的中线和高互相重合，故错误，是假命题；
B、等腰三角形的底角一定是锐角，正确，是真命题；
C、有一条边相等的两个等边三角形是全等三角形，正确，是真命题；
D、顶角相等，底边上的高也相等的两个等腰三角形全等，正确，是真命题；
故选A．

点评本题考查了命题与定理的知识，解题的关键是能够了解等腰三角形的性质及等腰三角形的判定方法，难度不大．

练习册系列答案

一通百通小学毕业升学模拟测试卷系列答案

典元教辅小学毕业升学必备小升初押题卷系列答案

金榜夺冠真题卷系列答案

小升初综合素质检测卷系列答案

相关题目

18．

如图，鹏鹏将长方形纸片ABCD剪成三角形纸片DEF，若∠DEF+∠EDF=90°，则∠EFB+∠DFC的度数为90°．

19．用图象法解方程组$\left\{\begin{array}{l}{x-2y=4}\\{2x+y=4}\end{array}\right.$时，下列选项中的图象正确的是（　　）

16．

如图，在数轴上有a，b两个实数，则化简|b-a|+|a+b|的结果是（　　）

3．已知（-1，y₁），（0.5，y₂），（1.7，y₃）是直线y=-9x+b（b为常数）上的三个点，则y₁，y₂，y₃的大小关系是（　　）

y₃＞y₂＞y₁

y₁＞y₂＞y₃

y₁＞y₃＞y₂

y₃＞y₁＞y₂

13．若关于x的不等式组$\left\{\begin{array}{l}{\frac{x+15}{2}＞x-3}\\{\frac{2x+2}{3}＜x+a}\end{array}\right.$的解只有4个整数解，则a的取值范围是（　　）

20．$\sqrt{（-5）^{2}}$=5；144的平方根是±12；$\root{3}{-64}$=-4．

17．若a的倒数是它本身，b的平方根等于它本身，那么（a²+b）²的值是（　　）

18．

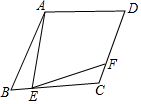如图，四边形ABCD是菱形．∠ABC=60°，点E是BC边上一点，∠AEF=60°，且EF交直线CD于点F，求证：AE=EF．

试题分类