题目内容
14.已知P1(-1,y1),P(-2,y2)是一次函数y=$\frac{1}{3}$x-1的图象上的两点,则y1与y2的大小关系是( )| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 以上都不对 |
分析 根据一次函数点的坐标特征即可求出y1与y2的值,比较后即可得出结论.(利用一次函数的单调性解决问题亦可)
解答 解:∵P1(-1,y1),P(-2,y2)是一次函数y=$\frac{1}{3}$x-1的图象上的两点,
∴y1=-$\frac{4}{3}$,y2=-$\frac{5}{3}$.
∵-$\frac{4}{3}$>-$\frac{5}{3}$,
∴y1>y2.
故选A.
点评 本题考查了一次函数图象上点的坐标特征,根据一次函数图象上点的坐标特征求出y1与y2的值是解题的关键.

练习册系列答案
相关题目
4.如图1,在平面直角坐标系中,将平行四边形ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2,那么平行四边形ABCD的面积为( )
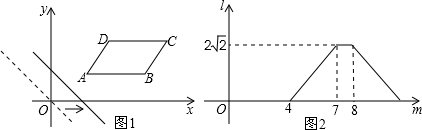

| A. | $4\sqrt{5}$ | B. | 4 | C. | $8\sqrt{5}$ | D. | 8 |
5. 如图是一个正方体的表面展开图,则在原正方体中与1所在的面相对的面上的数字为( )
如图是一个正方体的表面展开图,则在原正方体中与1所在的面相对的面上的数字为( )
 如图是一个正方体的表面展开图,则在原正方体中与1所在的面相对的面上的数字为( )
如图是一个正方体的表面展开图,则在原正方体中与1所在的面相对的面上的数字为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.下列计算正确的是( )
| A. | 2$\sqrt{2}$×3$\sqrt{3}$=6$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | 2$\sqrt{3}$-$\sqrt{3}$=2 | D. | 2÷$\sqrt{2}$=$\sqrt{2}$ |
9.已知关于x,y的方程组$\left\{\begin{array}{l}x+2y=m\\ y=2m\end{array}\right.$的解是二元一次方程-3x+4y=51的解,则m的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.一根铁丝正好围成一个长方形,一边长为2a+b,另一边比它长a-b,则长方形的周长为( )
| A. | 6a | B. | 10a+3b | C. | 10a+2b | D. | 10a+6b |
3.已知(-1,y1),(0.5,y2),(1.7,y3)是直线y=-9x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是( )
| A. | y3>y2>y1 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |




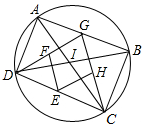 如图,AC与BD是⊙I的直径,AD=4,CD=10,点G是AB上一动点,点E、F、H分别是DC、DG、CG的中点.
如图,AC与BD是⊙I的直径,AD=4,CD=10,点G是AB上一动点,点E、F、H分别是DC、DG、CG的中点.