题目内容
18.在Rt△ABC中,∠C=90°,∠A的对边为a,∠B的对边为b,且满足a2-ab-b2=0,则tanA=( )| A. | 1 | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\frac{1-\sqrt{5}}{2}$ | D. | $\frac{1±\sqrt{5}}{2}$ |
分析 求出a=$\frac{1+\sqrt{5}}{2}$b,根据锐角三角函数的定义得出tanA=$\frac{a}{b}$,代入求出即可.
解答  解:a2-ab-b2=0,
解:a2-ab-b2=0,
(a-$\frac{1+\sqrt{5}}{2}$b)(a-$\frac{1-\sqrt{5}}{2}$b)=0,
则a=$\frac{1+\sqrt{5}}{2}$b,a=$\frac{1-\sqrt{5}}{2}$b(舍去),
则tanA=$\frac{a}{b}$=$\frac{1+\sqrt{5}}{2}$.
故选:B.
点评 本题考查了解二元二次方程和锐角三角函数的定义的应用,注意:tanA=$\frac{∠A的对边}{∠A的邻边}$.

练习册系列答案
相关题目
9.已知关于x,y的方程组$\left\{\begin{array}{l}x+2y=m\\ y=2m\end{array}\right.$的解是二元一次方程-3x+4y=51的解,则m的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.一根铁丝正好围成一个长方形,一边长为2a+b,另一边比它长a-b,则长方形的周长为( )
| A. | 6a | B. | 10a+3b | C. | 10a+2b | D. | 10a+6b |
13.计算(-4)2012×(-$\frac{1}{4}$)2011的结果是( )
| A. | 4 | B. | -4 | C. | 16 | D. | -16 |
3.已知(-1,y1),(0.5,y2),(1.7,y3)是直线y=-9x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是( )
| A. | y3>y2>y1 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
10.将平面直角坐标系中的点P(m-2,2m+1)向左平移1个单位后位于第二象限,则m的取值范围是( )
| A. | 0<m<2 | B. | -0.5<m<2 | C. | -0.5<m<1 | D. | -0.5<m<3 |
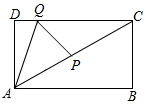 如图,长方形ABCD中,AD=a,DC=b,(a,b为常数),∠CAB=30°,点P是对角线AC的中点,点Q是线段CD上的动点,则AQ+QP的最小值为$\sqrt{3}a$.
如图,长方形ABCD中,AD=a,DC=b,(a,b为常数),∠CAB=30°,点P是对角线AC的中点,点Q是线段CD上的动点,则AQ+QP的最小值为$\sqrt{3}a$. 如图,在4×4的方格中有五个同样大小的正方形如图摆放,在其他空白方格中再任取一个涂上黑色,与其余五个正方形组成一个新图形.
如图,在4×4的方格中有五个同样大小的正方形如图摆放,在其他空白方格中再任取一个涂上黑色,与其余五个正方形组成一个新图形.