题目内容
13.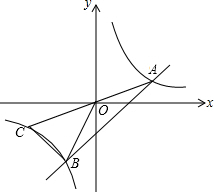 如图,直线y=x+b与双曲线y=$\frac{k}{x}$交于A、B两点,延长AO交双曲线于C点,连接BC,且AB=2BC=4$\sqrt{2}$,则k=3.
如图,直线y=x+b与双曲线y=$\frac{k}{x}$交于A、B两点,延长AO交双曲线于C点,连接BC,且AB=2BC=4$\sqrt{2}$,则k=3.
分析 过O作OD⊥AB于点D,根据直线y=x+b中的k=1得到OD所在直线为y=-x,于是得到直线y=x+b关于此直线轴对称,双曲线y=k/x关于O中心对称,求得AD=BD,AO=OC,根据平行线的性质得到BC⊥AC,设A(x,y)则B(-y,-x),根据勾股定理和两点间的距离公式得到(2x)2+(2y)2=(2$\sqrt{10}$)2,(x+y)2+(y+x)2=(4$\sqrt{2}$)2求得点A 坐标为(1,3)于是得到结论.
解答 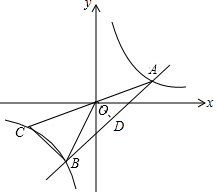 解:过O作OD⊥AB于点D,
解:过O作OD⊥AB于点D,
∴OD所在直线为y=-x,
∴直线y=x+b关于此直线轴对称,双曲线y=k/x关于O中心对称,
∴AD=BD,AO=OC,
∴OD∥BC,
∴BC⊥AC,
设A(x,y)则B(-y,-x),
∵AB=2BC=4$\sqrt{2}$,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{10}$,
∴(2x)2+(2y)2=(2$\sqrt{10}$)2,(x+y)2+(y+x)2=(4$\sqrt{2}$)2
解得x=1,y=3
∴点A 坐标为(1,3)
∴k=3.
故答案为:3.
点评 本题考查了反比例函数与一次函数的交点坐标,勾股定理,两点间的距离公式,正确的理解题意是解题的关键.

练习册系列答案
相关题目
3.已知(-1,y1),(0.5,y2),(1.7,y3)是直线y=-9x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是( )
| A. | y3>y2>y1 | B. | y1>y2>y3 | C. | y1>y3>y2 | D. | y3>y1>y2 |
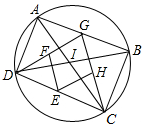 如图,AC与BD是⊙I的直径,AD=4,CD=10,点G是AB上一动点,点E、F、H分别是DC、DG、CG的中点.
如图,AC与BD是⊙I的直径,AD=4,CD=10,点G是AB上一动点,点E、F、H分别是DC、DG、CG的中点. 如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为$\sqrt{3}$.
如图,两个反比例函数y1=$\frac{{k}_{1}}{x}$(其中k1>0)和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2,点P在C1上,矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为$\sqrt{3}$. 如图,在4×4的方格中有五个同样大小的正方形如图摆放,在其他空白方格中再任取一个涂上黑色,与其余五个正方形组成一个新图形.
如图,在4×4的方格中有五个同样大小的正方形如图摆放,在其他空白方格中再任取一个涂上黑色,与其余五个正方形组成一个新图形.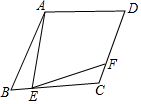 如图,四边形ABCD是菱形.∠ABC=60°,点E是BC边上一点,∠AEF=60°,且EF交直线CD于点F,求证:AE=EF.
如图,四边形ABCD是菱形.∠ABC=60°,点E是BC边上一点,∠AEF=60°,且EF交直线CD于点F,求证:AE=EF.