题目内容
5．在一个不透明的袋子里，有5个除颜色外，其他都相同的小球，其中有3个是红球，2个是绿球，每次拿一个球然后放回去，拿2次，则至少有一次取到绿球的概率是$\frac{16}{25}$．分析 列举出所有情况，数出至少有一次取到绿球的情况占总情况数的多少即可．
解答 解：列表如下：
| 红1 | 红2 | 红3 | 绿1 | 绿2 | |
| 红1 | （红1，红1） | （红1，红2） | （红1，红3） | （红1，绿1 ） | （红1，绿2） |
| 红2 | （红2，红1） | （红1，红2） | （红2，红3） | （红2，绿1） | （红2，绿2） |
| 红3 | （红3，红1） | （红3，红2） | （红3，红3） | （红3，绿1） | （红3，绿2） |
| 绿1 | （绿1，红1） | （绿1，红2） | （绿1，红3） | （绿1，绿1） | （绿1，绿2） |
| 绿2 | （绿2，红1） | （绿2，红2） | （绿2，红3） | （绿2，绿1） | （绿2，绿2） |
所以拿2次，则至少有一次取到绿球的概率=$\frac{16}{25}$，
故答案为：$\frac{16}{25}$．
点评 此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
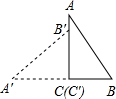如图，将一块斜边长为15cm，∠B=60°的直角三角板ABC，绕点C逆时针方向旋转90°至△A′B′C′的位置，再沿B′刚好落在斜边AB上，则此三角板向右平移的距离为$\frac{15}{2}$-$\frac{15\sqrt{3}}{2}$．
