题目内容
17.已知:a、b互为相反数,c、d互为倒数,|x|=2,且x>0,计算:(a+b)x2-cdx+x2的值.分析 根据互为相反数的两个数的和等于0可得a+b=0,互为倒数的两个数的乘积是1可得cd=1,绝对值的性质求出x,然后代入代数式进行计算即可得解.
解答 解:∵a、b互为相反数,
∴a+b=0,
∵c、d互为倒数,
∴cd=1,
∵|x|=2,且x>0,
∴x=2,
∴(a+b)x2-cdx+x2=0×22-1×2+22=0-2+4=2.
点评 本题考查了代数式求值,主要利用了相反数的定义,倒数的定义,绝对值的性质,熟记概念与性质是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
7.下列四组线段中,可以构成直角三角形的是( )
| A. | 5,6,7 | B. | 0.7,2.4,2.5 | C. | 1,1,2 | D. | 1,$\sqrt{2}$,3 |
9.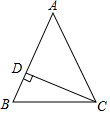 如图,等腰△ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
如图,等腰△ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
 如图,等腰△ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
如图,等腰△ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )| A. | 30° | B. | 25° | C. | 15° | D. | 20° |
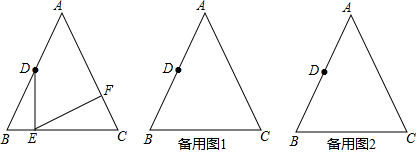
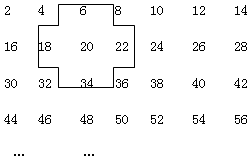 探索规律:将连续的偶数2,4,6,8,…,排成如表:
探索规律:将连续的偶数2,4,6,8,…,排成如表: