题目内容
2．
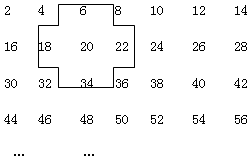探索规律：将连续的偶数2，4，6，8，…，排成如表：（1）若将十字框上下左右移动，可框住五位数，设中间的数为x，用代数式表示十字框中的五个数的和；
（2）若将十字框上下左右移动，可框住五位数的和能等于2000吗？如能，写出这五位数，如不能，说明理由．
分析 （1）根据上下的数相差14，左右的数相差2就可以求出5个数之和；
（2）根据框住五位数的和等于2000，列出方程得出中间的数，然后根据这个数确定它的位置就可以得出结论．
解答 解：（1）设中间的一个数为x，则其余的四个数分别为：x-14，x+14，x-2，x+2，
则十字框中的五个数之和为：x+x-14+x+14+x-2+x+2=5x，
（2）不可能
依题意有5x=2000，
解得x=400，
400÷2=200
200÷7=28…4
∵400在第4列，
∴400能成为十字框中的5个数的中间的数，
∴可框住五位数的和能等于2000．
点评 本题考查了一元一次方程的应用及一元一次方程的解法，在解答时求出中间的数与5个数的和的关系是关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
12．下列方程中，一元二次方程共有（ ）
①3x2+x=20；②x2-$\frac{1}{x}$=4；③2x2-3xy+4=0；④x2=1；⑤x2-$\frac{x}{3}$+3=0．
①3x2+x=20；②x2-$\frac{1}{x}$=4；③2x2-3xy+4=0；④x2=1；⑤x2-$\frac{x}{3}$+3=0．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
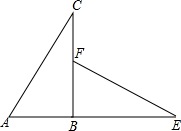如图，△ABC是直角三角形，延长AB到点E，使BE=BC，在BC上取一点F，使BF=AB，连接EF，△ABC旋转后能与△FBE重合，请回答：