题目内容
4.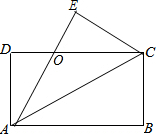 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
分析 根据折叠前后角相等可证AO=CO,在直角三角形ADO中,运用勾股定理求得DO,再根据线段的和差关系求解即可.
解答 解:根据折叠前后角相等可知∠BAC=∠EAC,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠BAC=∠ACD,
∴∠EAC=∠ACD,
∴AO=CO=5cm,
在直角三角形ADO中,DO=$\sqrt{A{O}^{2}-A{D}^{2}}$=3cm,
AB=CD=DO+CO=3+5=8cm.
故选:C.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况.
2011-2016年我国与东南亚地区和东欧地区的贸易额统计图
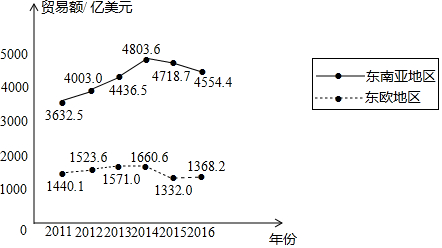
(以上数据摘自《“一带一路”贸易合作大数据报告(2017)》)
根据统计图提供的信息,下列推断不合理的是( )
2011-2016年我国与东南亚地区和东欧地区的贸易额统计图

(以上数据摘自《“一带一路”贸易合作大数据报告(2017)》)
根据统计图提供的信息,下列推断不合理的是( )
| A. | 与2015年相比,2016年我国与东欧地区的贸易额有所增长 | |
| B. | 2011-2016年,我国与东南亚地区的贸易额逐年增长 | |
| C. | 2011-2016年,我国与东南亚地区的贸易额的平均值超过4200亿美元 | |
| D. | 2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多 |
15.不等式组$\left\{\begin{array}{l}{3-2x<5}\\{x-2<1}\end{array}\right.$的解集为( )
| A. | x>-1 | B. | x<3 | C. | x<-1或x>3 | D. | -1<x<3 |
1.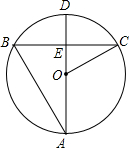 如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )
如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )
 如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )
如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
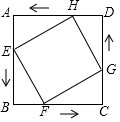 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为3s时,四边形EFGH的面积最小,其最小值是18cm2.
如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为3s时,四边形EFGH的面积最小,其最小值是18cm2.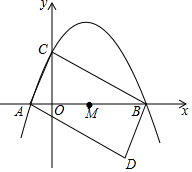 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.