题目内容
1.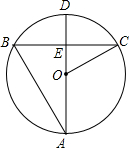 如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )
如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 如图,作辅助线;首先运用勾股定理求出AE的长度,然后运用射影定理求出AD的长度,即可解决问题.
解答  解:如图,连接BD;
解:如图,连接BD;
∵直径AD⊥BC,
∴BE=CE=$\frac{1}{2}$BC=6;
由勾股定理得:
AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=6$\sqrt{3}$;
∵AD为⊙O的直径,
∴∠ABD=90°;
由射影定理得:
AB2=AE•AD
∴AD=$\frac{1{2}^{2}}{6\sqrt{3}}$=8$\sqrt{3}$,
∴OC=$\frac{1}{2}$AD=4$\sqrt{3}$,
故选D.
点评 该题主要考查了垂径定理、射影定理等几何知识点及其应用问题;解题的方法是作辅助线,构造直角三角形;解题的关键是牢固掌握垂径定理、射影定理等几何知识点,这是灵活运用、解题的基础和关键.

练习册系列答案
相关题目
4.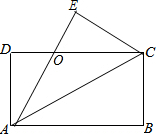 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
9.郴州市某景区的门票其票价如下:
今有甲乙两个旅游团均超过40人,且甲团人数少于乙团人数,两个团合在一起购票,总计付出门票费10080元.
(1)这两个旅游团共有多少人?
(2)若两旅游团分别购票,总计应付门票13140元,请问甲,乙两个旅游团各有多少人?
| 购票人数 | 1~49人 | 50~100人 | 100人以上 |
| 每人门票价 | 130元 | 110元 | 90元 |
(1)这两个旅游团共有多少人?
(2)若两旅游团分别购票,总计应付门票13140元,请问甲,乙两个旅游团各有多少人?
6. 如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
 如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )
如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
11.如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
(2)如果x节链条的总长度是y,求y与x之间的关系式;
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?

(1)观察图形填写下表:
| 链条节数(节) | 2 | 3 | 4 |
| 链条长度(cm) | 4.2 | 5.9 | 7.6 |
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?

 一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以v1的速度匀速跑至点B,原地休息半小时后,再以v2的速度匀速跑至终点C;乙以v3的速度匀速跑至终点C,甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象如图所示,则AB长为15千米,v1-v2=5千米/小时.
一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以v1的速度匀速跑至点B,原地休息半小时后,再以v2的速度匀速跑至终点C;乙以v3的速度匀速跑至终点C,甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象如图所示,则AB长为15千米,v1-v2=5千米/小时. 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论是①②③④⑤.
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论是①②③④⑤.