题目内容
12．
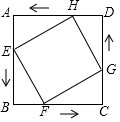如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s的速度向点B、C、D、A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为3s时，四边形EFGH的面积最小，其最小值是18cm2．
分析 设运动时间为t（0≤t≤6），则AE=t，AH=6-t，由四边形EFGH的面积=正方形ABCD的面积-4个△AEH的面积，即可得出S四边形EFGH关于t的函数关系式，配方后即可得出结论．
解答 解：设运动时间为t（0≤t≤6），则AE=t，AH=6-t，
根据题意得：S四边形EFGH=S正方形ABCD-4S△AEH=6×6-4×$\frac{1}{2}$t（6-t）=2t2-12t+36=2（t-3）2+18，
∴当t=3时，四边形EFGH的面积取最小值，最小值为18．
故答案为：3；18
点评 本题考查了二次函数的最值、三角形以及正方形的面积，通过分割图形求面积法找出S四边形EFGH关于t的函数关系式是解题的关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
2．下列运算正确的是（ ）
| A． | -3（x-4）=-3x+12 | B． | （-3x）2•4x2=-12x4 | C． | 3x+2x2=5x3 | D． | x6÷x2=x3 |
7．已知关于x的方程x2+x-a=0的一个根为2，则另一个根是（ ）
| A． | -3 | B． | -2 | C． | 3 | D． | 6 |
17．
阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表．
请根据图表中的信息，解答下列问题：
（1）表中的a=12，b=0.2，中位数落在1≤t≤1.5组，将频数分布直方图补全；
（2）估计该校2000名学生中，每周课余阅读时间不足0.5小时的学生大约有多少名？
（3）E组的4人中，有1名男生和3名女生，该校计划在E组学生中随机选出两人向全校同学作读书心得报告，请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率．
阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表．| 组别 | 时间（小时） | 频数（人数） | 频率 |
| A | 0≤t≤0.5 | 6 | 0.15 |
| B | 0.5≤t≤1 | a | 0.3 |
| C | 1≤t≤1.5 | 10 | 0.25 |
| D | 1.5≤t≤2 | 8 | b |
| E | 2≤t≤2.5 | 4 | 0.1 |
| 合计 | 1 |
（1）表中的a=12，b=0.2，中位数落在1≤t≤1.5组，将频数分布直方图补全；
（2）估计该校2000名学生中，每周课余阅读时间不足0.5小时的学生大约有多少名？
（3）E组的4人中，有1名男生和3名女生，该校计划在E组学生中随机选出两人向全校同学作读书心得报告，请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率．
4．
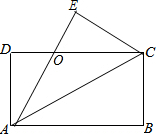如图，矩形纸片ABCD中，AD=4cm，把纸片沿直线AC折叠，点B落在E处，AE交DC于点O，若AO=5cm，则AB的长为（ ）
如图，矩形纸片ABCD中，AD=4cm，把纸片沿直线AC折叠，点B落在E处，AE交DC于点O，若AO=5cm，则AB的长为（ ）| A． | 6cm | B． | 7cm | C． | 8cm | D． | 9cm |
9．郴州市某景区的门票其票价如下：
今有甲乙两个旅游团均超过40人，且甲团人数少于乙团人数，两个团合在一起购票，总计付出门票费10080元．
（1）这两个旅游团共有多少人？
（2）若两旅游团分别购票，总计应付门票13140元，请问甲，乙两个旅游团各有多少人？
| 购票人数 | 1～49人 | 50～100人 | 100人以上 |
| 每人门票价 | 130元 | 110元 | 90元 |
（1）这两个旅游团共有多少人？
（2）若两旅游团分别购票，总计应付门票13140元，请问甲，乙两个旅游团各有多少人？
如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论是①②③④⑤．