题目内容
8.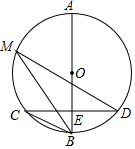 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.(1)判断BC、MD的位置关系,并说明理由;
(2)若AE=16,BE=4,求线段CD的长.
分析 (1)根据在同圆中,相等的圆周角所对的弧相等,相等的弧所对的圆周角相等,可以判断出BC、MD的位置关系;
(2)根据垂径定理和AE=16,BE=4,可以得到AB和OE的长度,然后根据勾股定理可以求得CE的长度,进而求得CD的长度.
解答 解:(1)BC、MD的位置关系是平行,
理由:∵∠M=∠D,
∴$\widehat{BD}=\widehat{MC}$,
∴∠M=∠MBC,
∴BC∥MD;
(2)连接OC,
∵AB是⊙O的直径,弦CD⊥AB于点E,AE=16,BE=4,
∴∠OEC=90°,EC=ED,AB=AE+BE=20,
∴OC=10,OE=OB-BE=6,
∴CE=$\sqrt{O{C}^{2}-O{E}^{2}}=8$,
∴CD=2CE=16,
即线段CD的长是16.
点评 本题考查圆周角定理、垂径定理、勾股定理,解题此类问题的关键是明确题意,根据所要证明或求解的问题找出相应的条件,利用圆周角定理、垂径定理和勾股定理的相关知识解答.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
16.老师布置了一个探究活动:仅用一架天平和若干个10克的砝码测量1元硬币和5角硬币的质量.(注:同种面值的每枚硬币质量相同).小海同学找来了足够多的1元硬币和5角硬币,经过实验探究,得到了如下的两个探究记录:
请你用所学的数学知识计算出一枚1元硬币多少克,一枚5角硬币多少克?
| 记录 | 天平左边 | 天平右边 | 天平状态 |
| 记录一 | 2枚1元硬币和7枚5角硬币 | 4个10克砝码 | 平衡 |
| 记录二 | 15枚1元硬币 | 20枚5角硬币和1个10克砝码 | 平衡 |
13.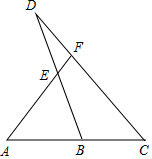 如图,B为AC的中点,E为BD的中点,则AF:AE为( )
如图,B为AC的中点,E为BD的中点,则AF:AE为( )
 如图,B为AC的中点,E为BD的中点,则AF:AE为( )
如图,B为AC的中点,E为BD的中点,则AF:AE为( )| A. | 4:3 | B. | 3:4 | C. | 1:2 | D. | 2:1 |
18.下列方程中,一元一次方程是( )
| A. | 2x=1 | B. | 3x-5 | C. | 3+7=10 | D. | x2+x=1 |
 如图,在四边形ABCD中,∠A=∠C,∠B=∠D,四边形ABCD是平行四边形吗?如果是,请说明理由,并且用文字语言叙述你的发现.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D,四边形ABCD是平行四边形吗?如果是,请说明理由,并且用文字语言叙述你的发现.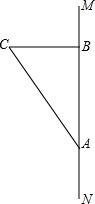 如图所示线段中,A、B为南北方向高速公路MN的两个出站口,A、B相距40km.风景区C在B的正西方向,司机小王由南向北到A后下高速路,沿老路AC到风景区C观光旅游后,再沿C到B后发现从A→C→B共走了50km,但小王不知道从C到B有多少公里,你能用数学知识帮他解决这个问题吗?请你写出求解过程.
如图所示线段中,A、B为南北方向高速公路MN的两个出站口,A、B相距40km.风景区C在B的正西方向,司机小王由南向北到A后下高速路,沿老路AC到风景区C观光旅游后,再沿C到B后发现从A→C→B共走了50km,但小王不知道从C到B有多少公里,你能用数学知识帮他解决这个问题吗?请你写出求解过程.