题目内容
4.如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=$\frac{角α的邻边}{角α的对边}$=$\frac{AC}{BC}$,根据上述角的余切定义,解下列问题:(1)如图1,若BC=3,AB=5,则ctanB=$\frac{3}{4}$;
(2)ctan60°=$\frac{\sqrt{3}}{3}$;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

分析 (1)先利用勾股定理计算出AC=4,然后根据余切的定义求解;
(2)根据余切的定义得到ctan60°=$\frac{1}{tan60°}$,然后把tan60°=$\sqrt{3}$代入计算即可;
(3)作AH⊥BC于H,如图2,先在Rt△ACH中利用余切的定义得到ctanC=$\frac{HC}{AH}$=2,则可设AH=x,CH=2x,BH=BC-CH=20-2x,接着再在Rt△ABH中利用勾股定理得到(20-2x)2+x2=102,解得x1=6,x2=10(舍去),所以BH=8,然后根据余弦的定义求解.
解答 解:(1)∵BC=3,AB=5,
∴AC=$\sqrt{{5}^{2}-{3}^{2}}$=4,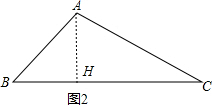
∴ctanB=$\frac{BC}{AC}$=$\frac{3}{4}$;
(2)ctan60°=$\frac{1}{tan60°}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$;
(3)作AH⊥BC于H,如图2,
在Rt△ACH中,ctanC=$\frac{HC}{AH}$=2,
设AH=x,则CH=2x,
∴BH=BC-CH=20-2x,
在Rt△ABH中,∵BH2+AH2=AB2,
∴(20-2x)2+x2=102,解得x1=6,x2=10(舍去),
∴BH=20-2×6=8,
∴cosB=$\frac{BH}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
 如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )
如图,四边形ABCD为平行四边形,EB⊥BC于B,ED⊥CD于D.若∠E=55°,则∠A的度数是( )| A. | 100° | B. | 110° | C. | 125° | D. | 135° |
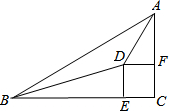 如图,△ABC中,∠C=90°,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F;
如图,△ABC中,∠C=90°,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F;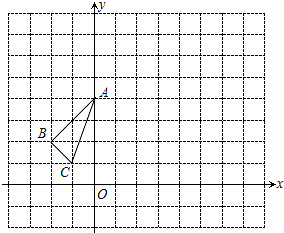 △ABC在平面直角坐标系中的位置如图所示,点O为坐标原点.
△ABC在平面直角坐标系中的位置如图所示,点O为坐标原点.