题目内容
16.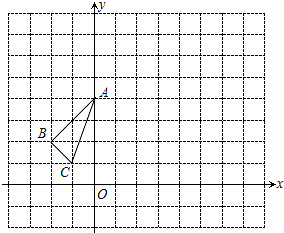 △ABC在平面直角坐标系中的位置如图所示,点O为坐标原点.
△ABC在平面直角坐标系中的位置如图所示,点O为坐标原点.(1)将△ABC向上平移3个单位长度,再向左平移1个单位长度,得到△A1B1C1;作△A1B1C1关于y轴对称的△A2B2C2;在图中画出△A1B1C1和△A2B2C2并写出A2、B2、C2的坐标.
(2)在y轴上存在一点M,使得△A1B1M的周长最小,请在图中画出点M的位置.
(3)将△ABC平移至点C与原点重合,在坐标轴上有点P,使得△ACP为等腰三角形,这样的P点有3个.
分析 (1)利用平移的性质以及轴对称的性质分别得出对应点位置进而得出答案;
(2)利用轴对称求最短路线的方法得出M点位置;
(3)利用等腰三角形的性质进而得出符合题意的答案.
解答  解:(1)如图所示:△A1B1C1和△A2B2C2即为所求;
解:(1)如图所示:△A1B1C1和△A2B2C2即为所求;
A2(1,7),B2(3,5),C2(2,4);
(2)如图所示:点M即为所求;
(3)如图所示:P,P′,P″即为所求,共3个点.
故答案为:3.
点评 此题主要考查了平移变换以及轴对称变换和利用轴对称求最短路线等知识,根据题意得出对应点位置是解题关键.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 全等三角形是指形状相同的两个三角形 | |
| B. | 全等三角形是指面积相等的两个三角形 | |
| C. | 周长和面积都相等的两个三角形全等 | |
| D. | 有两组角和一组边分别相等的两个三角形全等 |
1.抛物线y=$\frac{1}{2}$x2向下平移一个单位得到抛物线( )
| A. | y=$\frac{1}{2}$(x+1)2 | B. | y=$\frac{1}{2}$(x-1)2 | C. | y=$\frac{1}{2}$x2+1 | D. | y=$\frac{1}{2}$x2-1 |
5.某服装店进价为30元的内衣,以50元售出,平均每月能售出300件,经试销发现每件内衣每涨价10元,其月销售量就减少10件,为实现每月利润8700元,设定价为x元,则可得方程( )
| A. | 300(x-30)=8700 | B. | x(x-50)=8700 | ||
| C. | (x-30)[300-(x-50)]=8700 | D. | (x-30)(300-x)=8700 |
6.大于-1而小于$\sqrt{15}$的整数是( )
| A. | 0、1、2、3 | B. | 1、2、3 | C. | 2、3、4 | D. | 0、1、2、3、4 |
