题目内容
9.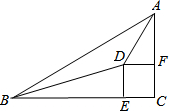 如图,△ABC中,∠C=90°,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F;
如图,△ABC中,∠C=90°,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F;(1)问四边形CFDE是正方形吗?请说明理由.
(2)若AC=6,BC=8,则CF的长为多少?
分析 (1)首先利用垂直的定义证得四边形CFDE是矩形,然后利用角平分线的性质得到DE=DF,从而判定该四边形是正方形.
(2)由勾股定理求出AB,由正方形的性质得出CF=DF=DE,设CF=DF=DE=x,则△ABC的面积=△ABD的面积+△BDE的面积+正方形CFDE的面积+△ADF的面积,解方程即可.
解答 解:(1)四边形CFDE是正方形,理由如下:
∵∠C=90°,DE⊥BC于点E,DF⊥AC于点F,
∴四边形DECF为矩形,
∵∠A、∠B的平分线交于点D,
∴D为△ABC的内心,
∴DF=DE,
∴四边形CFDE是正方形.
(2)∵∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵四边形CFDE是正方形,
∴CF=DF=DE,
设CF=DF=DE=x,
则△ABC的面积=△ABD的面积+△BDE的面积+正方形CFDE的面积+△ADF的面积
=$\frac{1}{2}$×10x+$\frac{1}{2}$(8-x)x+x2+$\frac{1}{2}$(6-x)x=$\frac{1}{2}$×6×8,
解得:x=2,
即CF的长为2.
点评 本题主要考查了角平分线的性质,三角形的内切圆与内心,解题的关键是利用正方形的判定方法证得四边形CFDE是正方形.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
14. 如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在外有一点F,使FA⊥AE,FC⊥BC.在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.有以下结论:①BE=CF;②ME⊥BC;③DE=DN;④图中度数为22.5°的角有5个,其中正确的结论有( )
如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在外有一点F,使FA⊥AE,FC⊥BC.在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.有以下结论:①BE=CF;②ME⊥BC;③DE=DN;④图中度数为22.5°的角有5个,其中正确的结论有( )
 如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在外有一点F,使FA⊥AE,FC⊥BC.在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.有以下结论:①BE=CF;②ME⊥BC;③DE=DN;④图中度数为22.5°的角有5个,其中正确的结论有( )
如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在外有一点F,使FA⊥AE,FC⊥BC.在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.有以下结论:①BE=CF;②ME⊥BC;③DE=DN;④图中度数为22.5°的角有5个,其中正确的结论有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
1.抛物线y=$\frac{1}{2}$x2向下平移一个单位得到抛物线( )
| A. | y=$\frac{1}{2}$(x+1)2 | B. | y=$\frac{1}{2}$(x-1)2 | C. | y=$\frac{1}{2}$x2+1 | D. | y=$\frac{1}{2}$x2-1 |
