题目内容
7. 如图,已知圆周角∠ACB的度数为100°,则圆周角∠D的度数等于80°.
如图,已知圆周角∠ACB的度数为100°,则圆周角∠D的度数等于80°.
分析 根据圆内接四边形的性质进行解答即可.
解答 解:∵四边形ABCD内接⊙O,
∴∠D+∠BCA=180°,
∴∠D=180°-∠ACB=180°-100°=80°.
故答案为:80°.
点评 本题考查的是圆内接四边形的性质,即圆内接四边形的对角互补,属于基础题,直接利用定理即可求解.

练习册系列答案
相关题目
18. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
2.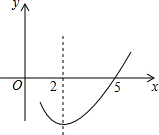 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
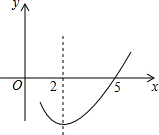 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(5,0),对称轴为直线x=2,则下列结论中正确的是( )| A. | 当x>2时,y随x增大而减小 | B. | 4a=b | ||
| C. | 图象过点(-1,0) | D. | 9a+3b+c>0 |
12.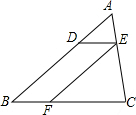 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
 如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )
如图,在△ABC中,点D在边AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,△EFC的面积记为S1,四边形DEFB的面积为S2.若$\frac{AD}{DB}=\frac{1}{2}$,则S1与S2的大小关系为( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 2S1=S2 |
16.下列函数,一定是二次函数的是( )
| A. | y=x2-$\frac{1}{x}$ | B. | y=ax2+bx+c | C. | y=(x-3)2-x2 | D. | y=(m2+1)x2(m为常数) |
 如图,直线l1∥l2,AC=10,DE=3,EF=2,则AB的长是6.
如图,直线l1∥l2,AC=10,DE=3,EF=2,则AB的长是6.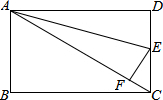 已知:如图,长方形ABCD中,AB=6,AD=8,沿直线AE把△ADE折叠,点O恰好落在AC上一点F处.
已知:如图,长方形ABCD中,AB=6,AD=8,沿直线AE把△ADE折叠,点O恰好落在AC上一点F处.