题目内容
3.已知等腰三角形一腰上的中线将这个三角形的周长分成12和9两部分,求这个等腰三角形的腰长和底边长.分析 设腰长为x,底边长为y,根据等腰三角形一腰上的中线将这个等腰三角形的周长分为9和12两部分,列方程解得即可.
解答 解:设腰长为x,底边长为y,
则$\left\{\begin{array}{l}{x+\frac{x}{2}=12}\\{y+\frac{x}{2}=9}\end{array}\right.或\left\{\begin{array}{l}{x+\frac{x}{2}=9}\\{y+\frac{x}{2}=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=5}\end{array}\right.或\left\{\begin{array}{l}{x=6}\\{y=9}\end{array}\right.$,
经检验,都符合三角形的三边关系.
因此三角形的底边长为9cm或5cm,等腰三角形的腰长为6cm或8cm.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确3:2两部分是哪一部分含有底边,所以一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
相关题目
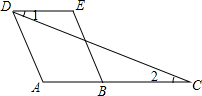 请将下列推理过程补充完整.
请将下列推理过程补充完整.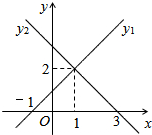 如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.
如图,已知一次函数y1=kx1+b1与一次函数y2=kx2+b2的图象相交于点(1,2),则不等式kx1+b1<kx2+b2的解集是x<1.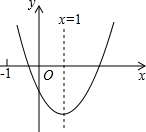 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论: