题目内容
5.(1)解方程:$\frac{x-2}{x+2}$-$\frac{12}{{x}^{2}-4}$=1(2)先化简,再求值:$\frac{2a+6}{{a}^{2}-4a+4}$$•\frac{a-2}{{a}^{2}+3a}$-$\frac{1}{a-2}$,其中a=-cos45°.
分析 (1)先去分母,把分式方程化为一元一次方程得到(x-2)2-12=x2-4,然后解一元一次方程后进行检验,最后确定原方程的解;
(2)先把分子分母分解因式,约分后进行通分,化简得到原式=-$\frac{1}{a}$,然后把a=-$\frac{\sqrt{2}}{2}$代入计算即可.
解答 解:(1)去分母得(x-2)2-12=x2-4,
解得x=-1,
检验:当x=-1时,(x+2)(x-2)≠0,
所以原方程的解为x=-1;
(2)原式=$\frac{2(a+3)}{(a-2)^{2}}$•$\frac{a-2}{a(a+3)}$-$\frac{1}{a-2}$
=$\frac{2}{a(a-2)}$-$\frac{a}{a(a-2)}$
=$\frac{-(a-2)}{a(a-2)}$
=-$\frac{1}{a}$,
当a=-cos45°=-$\frac{\sqrt{2}}{2}$时,原式=-$\frac{1}{-\frac{\sqrt{2}}{2}}$=$\sqrt{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了解分式方程.

练习册系列答案
相关题目
14.计算$\frac{x-2}{2}$$÷(1-\frac{2}{x})$,所得的正确结果是( )
| A. | $\frac{1}{2}$x | B. | -$\frac{1}{x}$ | C. | $\frac{1}{x}$ | D. | -$\frac{x-2}{x}$ |
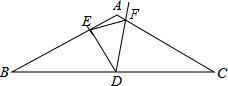 已知:△ABC中,AB=AC,∠BAC=120°,D为BC的中点,且∠EDF=∠C.
已知:△ABC中,AB=AC,∠BAC=120°,D为BC的中点,且∠EDF=∠C.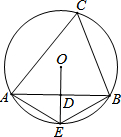 如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE;②AE=BE;③OD=DE;④∠AEO=∠C;⑤$\widehat{AE}$=$\frac{1}{2}$$\widehat{AEB}$.正确结论的个数是( )
如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE;②AE=BE;③OD=DE;④∠AEO=∠C;⑤$\widehat{AE}$=$\frac{1}{2}$$\widehat{AEB}$.正确结论的个数是( )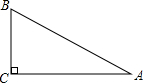 如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.
如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.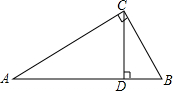 如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,DB=1cm.求:
如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,DB=1cm.求: