题目内容
10.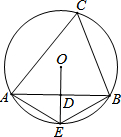 如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE;②AE=BE;③OD=DE;④∠AEO=∠C;⑤$\widehat{AE}$=$\frac{1}{2}$$\widehat{AEB}$.正确结论的个数是( )
如图,△ABC内接于⊙O,D为线段AB的中点,延长OD交⊙O于点E,连接AE,BE,则下列五个结论①AB⊥DE;②AE=BE;③OD=DE;④∠AEO=∠C;⑤$\widehat{AE}$=$\frac{1}{2}$$\widehat{AEB}$.正确结论的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 已知OE是⊙O的半径,D是弦AB的中点,可根据垂径定理的推论来判断所给出的结论是否正确.
解答 解:∵OE是⊙O的半径,且D是AB的中点,
∴OE⊥AB,$\widehat{AE}$=$\widehat{BE}$=$\frac{1}{2}$$\widehat{AEB}$;(故①⑤正确)
∴AE=BE;(故②正确)
由于没有条件能够证明③④一定成立,所以一定正确的结论是①②⑤;
故选B.
点评 本题考查的是垂径定理,涉及到了圆心角、弧、弦的关系及垂径定理的推论;垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两段弧.

练习册系列答案
相关题目
19.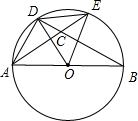 如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
 如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )
如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠DEA相等的角有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 个 |
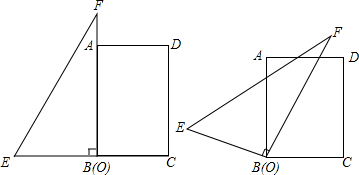
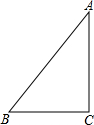 如图是一个直角三角形纸片,其中∠C=90°,两直角边长分别为3cm,4cm,现要给这个纸片再拼接一个直角三角形纸片,两纸片不重叠且无缝隙,使得拼接后的纸片形状是等腰三角形,拼接成的等腰三角形的纸片的周长为16或18cm.
如图是一个直角三角形纸片,其中∠C=90°,两直角边长分别为3cm,4cm,现要给这个纸片再拼接一个直角三角形纸片,两纸片不重叠且无缝隙,使得拼接后的纸片形状是等腰三角形,拼接成的等腰三角形的纸片的周长为16或18cm.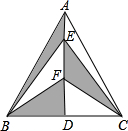 如图,在面积为4的等边三角形ABC中,AD是BC边上的高,点E、F是AD上的两点,则图中阴影部分的面积是2$\sqrt{3}$.
如图,在面积为4的等边三角形ABC中,AD是BC边上的高,点E、F是AD上的两点,则图中阴影部分的面积是2$\sqrt{3}$.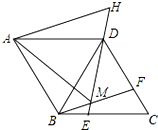 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论: