题目内容
如图，抛物线y=x2 +bx+c与x轴交于A（﹣1，0），B（3，0）两点．
（1）求该抛物线的解析式；
（2）求该抛物线的对称轴以及顶点坐标；
（3）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．
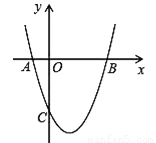
（1）y=x2﹣2x﹣3；（2）抛物线的对称轴x=1，顶点坐标（1，﹣4）；（3）（，4）或（，4）或（1，﹣4）．
【解析】试题分析：（1）由于抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3，然后利用根与系数即可确定b、c的值．
（2）根据S△PAB=8，求得P的纵坐标，把纵坐标代入抛物线的解析式即可求得...
天天向上一本好卷系列答案
小学生10分钟应用题系列答案如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升3m时，水面CD的宽是10m，建立如图所示的直角坐标系，则此抛物线的解析式为___________．
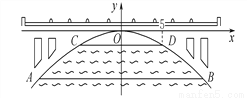
y＝－x2
【解析】【解析】
设抛物线解析式为y=ax2，因为抛物线关于y轴对称，AB=20，所以点B的横坐标为10．设点B（10，n），点D（5，n+3），由题意得： ，解得： ，∴．
故答案为： ． 如图为某菜农搭建的一个横截面为抛物线的大棚，有关尺寸如图所示，某菜农身高1.6米，则他在不弯腰的情况下在大棚内左右活动的范围是( )
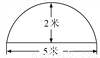
A.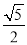 
米 B.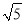 
米 C. 1.6米 D. 0.8米
B
【解析】如图，设抛物线的解析式为y=a（x-2.5）2+2，由待定系数法求出抛物线的解析式y=- （x-2.5）2+2，将y=1.6时代入解析式得- （x-2.5）2+2=1.6，解得， ，他在不弯腰的情况下在大棚里活动的范围是：x1-x2=．
故选：B. 在平面直角坐标系中，线段OP的两个端点坐标分别为O（0，0），P（4， 3），将线段OP绕点O逆时针旋转90°到OP′位置，则点P′的坐标是（ ）
A．（3，4） B．（－4，3） C．（－3，4） D．（4，－3）
C．
【解析】
试题分析：如图，OA=3，PA=4，
把线段OP绕点O逆时针旋转90°到OP′位置可得OA旋转到x轴负半轴OA′的位置，OB旋转到y轴正半轴OB′的位置,所以P′A′=PA=4，P′B′=PB=3,即可得P′点的坐标为（﹣3，4）．故答案选C． 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（ ）
A. 
B. 
C. 
D. 
B
【解析】试题解析：A、不是中心对称图形，本选项错误；
B、是中心对称图形，本选项正确；
C、不是中心对称图形，本选项错误；
D、不是中心对称图形，本选项错误．
故选B． 二次函数y=x2+bx+c的图象经过点（4，3），（3，0）．
（1）求b、c的值；
（2）求该二次函数图象的顶点坐标和对称轴．
（1） ；（2）顶点坐标为（2，﹣1），对称轴为直线x=2
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式.
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴ ，
解得 ；
（2）∵该二次函数为y=x2﹣4x+3=（x... 如图是二次函数y=ax2+bx+c图象的一部分，其对称轴是x=﹣1，且过点（﹣3，0），下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（3，y2）是抛物线上两点，则y1＜y2，其中说法正确的是（ ）
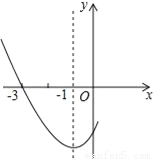
A. ①② B. ②③ C. ①②④ D. ②③④
A
【解析】∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；
∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；
∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；
∵点（﹣5，y1）离对称轴的距离与点（3，y2）离对称轴的距离相等，∴y1=y2，所以④不正确．
故选：A． 若等腰三角形有两条边的长度为2和5，则此等腰三角形的周长为（ ）
A. 9 B. 12 C. 9或12 D. 10
B
【解析】由于等腰三角形的底边不确定，所以需要分类讨论，
①当底边长为2时，三边长为2，5，5，则周长为2+5+5=12；
②当底边长为5时，三边长为5，2，2，但5＞2+2，不能构成三角形.
故选B. 如图，抛物线y=x2 +bx+c与x轴交于A（﹣1，0），B（3，0）两点．
（1）求该抛物线的解析式；
（2）求该抛物线的对称轴以及顶点坐标；
（3）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．
（1）y=x2﹣2x﹣3；（2）抛物线的对称轴x=1，顶点坐标（1，﹣4）；（3）（，4）或（，4）或（1，﹣4）．
【解析】试题分析：（1）由于抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3，然后利用根与系数即可确定b、c的值．
（2）根据S△PAB=8，求得P的纵坐标，把纵坐标代入抛物线的解析式即可求得...