题目内容
三角形的一边上有一点，它到三个顶点的距离相等，则这个三角形是_______三角形．
直角
【解析】∵直角三角形斜边上的中线等于斜边的一半，
∴这个三角形是直角三角形.
故答案为：直角.
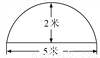
黄冈天天练口算题卡系列答案如图为某菜农搭建的一个横截面为抛物线的大棚，有关尺寸如图所示，某菜农身高1.6米，则他在不弯腰的情况下在大棚内左右活动的范围是( )
A.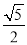 
米 B.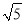 
米 C. 1.6米 D. 0.8米
B
【解析】如图，设抛物线的解析式为y=a（x-2.5）2+2，由待定系数法求出抛物线的解析式y=- （x-2.5）2+2，将y=1.6时代入解析式得- （x-2.5）2+2=1.6，解得， ，他在不弯腰的情况下在大棚里活动的范围是：x1-x2=．
故选：B. 如图是二次函数y=ax2+bx+c图象的一部分，其对称轴是x=﹣1，且过点（﹣3，0），下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（3，y2）是抛物线上两点，则y1＜y2，其中说法正确的是（ ）
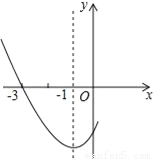
A. ①② B. ②③ C. ①②④ D. ②③④
A
【解析】∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；
∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；
∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；
∵点（﹣5，y1）离对称轴的距离与点（3，y2）离对称轴的距离相等，∴y1=y2，所以④不正确．
故选：A． 若等腰三角形有两条边的长度为2和5，则此等腰三角形的周长为（ ）
A. 9 B. 12 C. 9或12 D. 10
B
【解析】由于等腰三角形的底边不确定，所以需要分类讨论，
①当底边长为2时，三边长为2，5，5，则周长为2+5+5=12；
②当底边长为5时，三边长为5，2，2，但5＞2+2，不能构成三角形.
故选B. 已知：如图，△ABC的∠B、∠C的平分线相交于点D，过D作MN∥BC交AB、AC分别于点M、N，求证：BM＋CN＝MN.
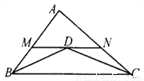
见解析
【解析】试题分析：根据角平分线的定义可得∠1=∠2，∠3=∠4，再根据两直线平行，内错角相等可得∠6=∠2，∠3=∠5，然后求出∠1=∠6，∠4=∠5，根据等角对等边的性质可得BM=DM，CN=DN，然后列式求解即可得证．
试题解析：证明：
∵BD、CF平分∠ABC、∠ACB，
∴∠1=∠2，∠3=∠4，
∵MN∥BC，
∴∠6=∠2，∠3=∠5，
... 如果△ABC中，两边a＝7cm，b＝3cm，则c的取值范围是_________；第三边为奇数的所有可能值为_________；周长为偶数的所有可能值为_________．
4cm＜c＜10cm 5cm、7cm、9cm 16cm或18cm
【解析】根据三角形的三边关系，得7cm?3cm下列判断正确的是( )
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 有两边对应相等，且有一角为30°的两个等腰三角形全等
C. 有一角和一条边对应相等的两个直角三角形全等
D. 有两角和一边对应相等的两个三角形全等
D
【解析】A.只有两个三角形同为锐角三角形或者钝角三角形或者直角三角形时，才能成立；
B. 30°角没有对应关系，不能成立；
C.如果这个角是直角，此时就不成立了；
D.符合全等三角形的判断方法：AAS或者ASA.
故选：D. 如图，抛物线y=x2 +bx+c与x轴交于A（﹣1，0），B（3，0）两点．
（1）求该抛物线的解析式；
（2）求该抛物线的对称轴以及顶点坐标；
（3）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．
（1）y=x2﹣2x﹣3；（2）抛物线的对称轴x=1，顶点坐标（1，﹣4）；（3）（，4）或（，4）或（1，﹣4）．
【解析】试题分析：（1）由于抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3，然后利用根与系数即可确定b、c的值．
（2）根据S△PAB=8，求得P的纵坐标，把纵坐标代入抛物线的解析式即可求得... 下列关于函数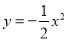
的图象说法：①图象是一条抛物线；②开口向下；③对称轴是y轴；④顶点（0，0），其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
D
【解析】
试题分析：函数是一种最基本的二次函数，画出图象，直接可知：
② 二次函数的图象是抛物线，正确；
②因为a=﹣＜0，抛物线开口向下，正确；
③因为b=0，对称轴是y轴，正确；
④顶点（0，0）也正确．
故选D．