题目内容
9. 如图所示,△ABD≌△ACD,∠BAC=90°.
如图所示,△ABD≌△ACD,∠BAC=90°.(1)求∠B;
(2)判断AD与BC的位置关系,并说明理由.
分析 (1)先根据全等三角形的性质得出∠A与∠B的关系,再根据∠BAC的度数求得∠B的度数;
(2)先根据全等三角形的性质得出∠BDA与∠CDA的关系,再根据∠BDC为平角,求得∠BDA的度数,即可得出结论.
解答 解:(1)∵△ABD≌△ACD,
∴∠B=∠C,
又∵∠BAC=90°,
∴∠B=∠C=45°;
(2)AD⊥BC.
理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA,
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,
∴AD⊥BC.
点评 本题主要考查了全等三角形的性质以及垂线的定义.解题时注意,全等三角形的对应角相等,对应边也相等.

练习册系列答案
相关题目
19.若a>b,则下列式子中一定成立的是( )
| A. | a-2<b-2 | B. | $\frac{a}{2}$>$\frac{b}{2}$ | C. | 2a>b | D. | 3-a>3-b |
20.方程2x+3y=15的正整数解有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
1.如果反比例函数y=$\frac{k}{x}$的图象经过点(3,-2),则k的值是( )
| A. | -6 | B. | 6 | C. | -3 | D. | 3 |
18.若点M(1-m,2+m)在第四象限,则m的取值范围是( )
| A. | m<1 | B. | m>-2 | C. | m<-2 | D. | -2<m<1 |
 △ABC的位置如图所示:
△ABC的位置如图所示: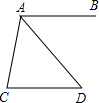 如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D的度数为50°.
如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D的度数为50°.