题目内容
8. 我们定义:有一组对角相等而另一组对角不相等的四边形叫做“等对角四边形”
我们定义:有一组对角相等而另一组对角不相等的四边形叫做“等对角四边形”(1)已知:四边形ABCD是“等对角四边形”,∠A=70°,∠B=80°,求∠C、∠D的度数
;
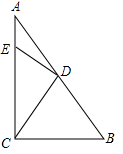
(2)如图,在Rt△ACB中,∠C=90°,CD为斜边AB上的中线,过点D作DE⊥CD交AC于点E,求证:四边形BCED是“等对角四边形”.
分析 (1)根据“等对角四边形”的定义,当四边形ABCD是“等对角四边形”时,可分两种情况进行讨论:①若∠A=∠C,∠B≠∠D,则∠C=70°,再利用四边形内角和定理求出∠D;②若∠B=∠D,∠A≠∠C,则∠D=80°,再利用四边形内角和定理求出∠C;
(2)根据直角三角形斜边上的中线等于斜边的一半得出AD=DB=DC,由等边对等角得出∠DCB=∠B,再由∠B+∠ACD=∠DCB+∠ACD=90°,∠CED+∠ACD=90°,利用同角的余角相等得出∠CED=∠B,又∠ECB≠∠EDB,根据“等对角四边形”的定义,即可证明四边形BCED是“等对角四边形”.
解答 (1)解:①若∠A=∠C,∠B≠∠D,
则∠C=70°,∠D=360°-70°-70°-80°=140°;
②若∠B=∠D,∠A≠∠C,
则∠D=80°,∠C=360°-80°-80°-70°=130°;
(2)证明:在Rt△ABC中,
∵CD为斜边AB边上的中线,
∴AD=DB=DC,
∴∠DCB=∠B,
∵∠ACB=90°,
∴∠DCB+∠ACD=90°,
∴∠B+∠ACD=90°.
∵DE⊥CD,
∴∠CED+∠ACD=90°,
∴∠CED=∠B,
且∠ECB≠∠EDB,
∴四边形BCED是“等对角四边形”.
点评 本题主要考查了四边形内角和定理,直角三角形、等腰三角形的性质,余角的性质,理解“等对角四边形”的定义并且利用分类讨论思想是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
13.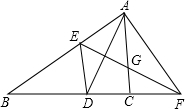 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点E,交AC于点G,交BC的延长线于点F,连接AF、DE,下列结论:①△AEF≌△DEF②CF=AF-CD③DE∥AC④△AEG为等边三角形,其中正确结论有( )
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点E,交AC于点G,交BC的延长线于点F,连接AF、DE,下列结论:①△AEF≌△DEF②CF=AF-CD③DE∥AC④△AEG为等边三角形,其中正确结论有( )
 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点E,交AC于点G,交BC的延长线于点F,连接AF、DE,下列结论:①△AEF≌△DEF②CF=AF-CD③DE∥AC④△AEG为等边三角形,其中正确结论有( )
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点E,交AC于点G,交BC的延长线于点F,连接AF、DE,下列结论:①△AEF≌△DEF②CF=AF-CD③DE∥AC④△AEG为等边三角形,其中正确结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.将七年级两个班男生掷实心球的成绩进行整理,并绘制出频数分布表、扇形统计图和频数分布直方图(不完整).(x表示成绩,且规定x≥6.25为合格,x≥9.25为优秀)

(1)频数分布表中,a=15,b=5,其中成绩合格的有45人,请补全频数分布直方图;
(2)扇形统计图中E组对应的圆心角是36°.
| 组别 | 成绩(米) | 频数 |
| A | 5.25≤x<6.25 | 5 |
| B | 6.25≤x<7.25 | 10 |
| C | 7.25≤x<8.25 | a |
| D | 8.25≤x<9.25 | 15 |
| E | 9.25≤x<10.25 | b |

(1)频数分布表中,a=15,b=5,其中成绩合格的有45人,请补全频数分布直方图;
(2)扇形统计图中E组对应的圆心角是36°.
 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离s (km)与甲车行驶的时间t(h)之间的函数关系如图所示.
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离s (km)与甲车行驶的时间t(h)之间的函数关系如图所示.
 如图,将一张长方形纸条折叠,则∠1=64度.
如图,将一张长方形纸条折叠,则∠1=64度.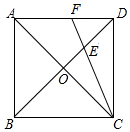 如图,正方形ABCD的对角线交于点O,∠ACD的平分线交BD、AD于点E、F,若正方形的边长为1,则AF=2-$\sqrt{2}$.
如图,正方形ABCD的对角线交于点O,∠ACD的平分线交BD、AD于点E、F,若正方形的边长为1,则AF=2-$\sqrt{2}$.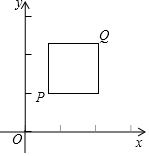 在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.
在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.