题目内容
15. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离s (km)与甲车行驶的时间t(h)之间的函数关系如图所示.
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离s (km)与甲车行驶的时间t(h)之间的函数关系如图所示.(1)请分别求出甲、乙两车离开A城的距离s (km)与甲车行驶的时间t(h)之间的函数表达式;
(2)当甲乙两车都在行驶过程中时,甲车出发多长时间,两车相距50千米.
分析 (1)根据图象中的信息分别求出甲乙两车对应的函数解析式,
(2)根据(1)中的函数解析式,可知它们相遇前和相遇后两种情况相距50千米,从而可以解答本题.
解答 解:(1)设甲对应的函数解析式为:y=kt,
300=5k
解得,k=60,
即甲对应的函数解析式为:y=60t,
设乙对应的函数解析式为y=mt+n,
$\left\{\begin{array}{l}{m+n=0}\\{4m+n=300}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{m=100}\\{n=-100}\end{array}\right.$,
即乙对应的函数解析式为y=100t-100,
(2)由题意可得,
当乙出发前甲、乙两车相距50千米,则50=60t,得t=$\frac{5}{6}$,
当乙出发后到乙到达终点的过程中,则60t-(100t-100)=±50,
解得,t=1.25或t=3.75,
当乙到达终点后甲、乙两车相距50千米,则300-50=60t,得x=$\frac{25}{6}$,
即$\frac{5}{6}$小时、1.25小时、3.75小时、$\frac{25}{6}$小时时,甲、乙两车相距50千米.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
5.已知反比例函数y=$\frac{6}{x}$,在下列结论中,错误的是( )
| A. | 图象位于第一、三象限 | B. | 图象必经过点(-2,-3) | ||
| C. | y随x的增大而增大 | D. | 若x>2,则y<3 |
7.一个两位数的两个数字之和为11,两个数字之差为5.求这个两位数,此题的解( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 4个 |

 尺规作图
尺规作图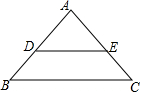 如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( )
如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( )
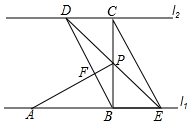 如图,直线l1∥l2,线段AB在l1上,BC⊥l1交l2于点C,且AB=BC=2cm,点P在点B、C之间,过点P的直线分别交l2、l1于点D、E;已知∠CDP=45°.
如图,直线l1∥l2,线段AB在l1上,BC⊥l1交l2于点C,且AB=BC=2cm,点P在点B、C之间,过点P的直线分别交l2、l1于点D、E;已知∠CDP=45°. 我们定义:有一组对角相等而另一组对角不相等的四边形叫做“等对角四边形”
我们定义:有一组对角相等而另一组对角不相等的四边形叫做“等对角四边形”