题目内容
13.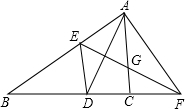 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点E,交AC于点G,交BC的延长线于点F,连接AF、DE,下列结论:①△AEF≌△DEF②CF=AF-CD③DE∥AC④△AEG为等边三角形,其中正确结论有( )
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点E,交AC于点G,交BC的延长线于点F,连接AF、DE,下列结论:①△AEF≌△DEF②CF=AF-CD③DE∥AC④△AEG为等边三角形,其中正确结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由垂直平分线的性质可求得AE=DE、AF=DF,则可证得△AEF≌△DEF,可判断①;由①可得AF=DF,则可判断②;由角平分线和①的结论,可证DE∥AC,可判断③;利用题目条件无法判断④正确;可得出答案.
解答 解:
∵EF垂直平分AD,
∴AE=DE,AF=DF,
在△AEF和△DEF中
$\left\{\begin{array}{l}{AE=DE}\\{AF=DF}\\{EF=EF}\end{array}\right.$
∴△AEF≌△DEF(SSS),故①正确;
∵DF=DC+CF,
∴CF=DF-CD=AF-CD,故②正确;
∵AD平分∠BAC,
∴∠EAD=∠CAD,且∠EAD=∠EDA,
∴∠EDA=∠CAD,
∴DE∥AC,故③正确;
当△AEG为等边三角形时,则∠AEG=∠DEG=∠BED=60°,
∠AFE=∠DFE=∠B=30°,则△ABC为直角三角形,而题目条件中没有该条件,
即由题目条件无法得出△AEG为等边三角形,故④不正确;
综上可知正确的结论有3个,
故选C.
点评 本题主要考查全等三角形的判定和性质,利用线段垂直平分线的性质得到AE=DE、AF=DF是解题的关键.

练习册系列答案
相关题目
5.某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.[毛利润=(售价-进价)×销售量]
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
| A | B | |
| 进价(万元/套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
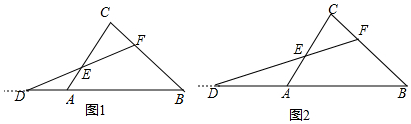
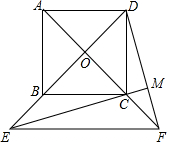 如图,正方形ABCD的对角线AC、BD相交于点O,点E在DB的延长线上,连接EC.过点D作DM⊥EC,垂足为M,DM与AC相交于点F,连接EF.求证:
如图,正方形ABCD的对角线AC、BD相交于点O,点E在DB的延长线上,连接EC.过点D作DM⊥EC,垂足为M,DM与AC相交于点F,连接EF.求证: 如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.
如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.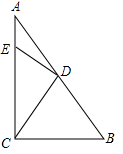 我们定义:有一组对角相等而另一组对角不相等的四边形叫做“等对角四边形”
我们定义:有一组对角相等而另一组对角不相等的四边形叫做“等对角四边形”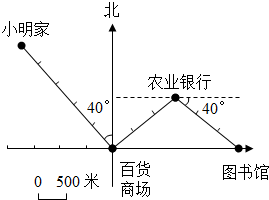 小明家在百货商场的北偏西40°方向2500米处,图书馆在农业银行东偏南40°方向1500米处,如图是小明坐出租车从家去图书馆的路线图,已知出租车在3千米以内(含3千米)按起步价9元计算,以后每增加1千米车费就增加2元.请你按图中提供的信息算一算,小明一共要花多少元出租车费?
小明家在百货商场的北偏西40°方向2500米处,图书馆在农业银行东偏南40°方向1500米处,如图是小明坐出租车从家去图书馆的路线图,已知出租车在3千米以内(含3千米)按起步价9元计算,以后每增加1千米车费就增加2元.请你按图中提供的信息算一算,小明一共要花多少元出租车费?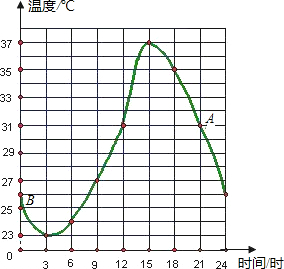 如图是某地某天温度变化的情况,根据图象回答问题:
如图是某地某天温度变化的情况,根据图象回答问题: