题目内容
20.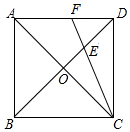 如图,正方形ABCD的对角线交于点O,∠ACD的平分线交BD、AD于点E、F,若正方形的边长为1,则AF=2-$\sqrt{2}$.
如图,正方形ABCD的对角线交于点O,∠ACD的平分线交BD、AD于点E、F,若正方形的边长为1,则AF=2-$\sqrt{2}$.
分析 作垂线段FG,根据角平分线的性质得:FG=DF,设AF=x,则FG=DF=1-x,在Rt△AGF中,由勾股定理列方程可得结论.
解答 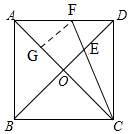 解:过F作FG⊥AC于G,
解:过F作FG⊥AC于G,
∵四边形ABCD是正方形,
∴∠ADC=90°,
∵CE平分∠ACD,
∴FG=DF,
∵CF=CF,
∴Rt△GFC≌Rt△DFC(HL),
∴CG=DC=1,
在Rt△ACD中,由勾股定理得:AC=$\sqrt{2}$,
∴AG=$\sqrt{2}$-1,
设AF=x,则FG=DF=1-x,
在Rt△AGF中,由勾股定理得:AF2=AG2+GF2,
∴x2=($\sqrt{2}$-1)2+(1-x)2,
x=2-$\sqrt{2}$,
即AF=2-$\sqrt{2}$,
故答案为:2-$\sqrt{2}$.
点评 本题考查了正方形的性质,角平分线的性质,直角三角形全等的性质和判定、勾股定理,熟记各性质与定理是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
15.计算(27a8)÷($\frac{1}{3}{a}^{3}$)÷(9a2)的顺序不正确的是( )
| A. | (27a8)÷[($\frac{1}{3}{a}^{3}$)÷(9a2)] | B. | [(27a8)÷($\frac{1}{3}{a}^{3}$)]÷(9a2) | C. | (27$÷\frac{1}{3}÷9$)a8-3-2 | D. | [(27a3)÷(9a2)]÷($\frac{1}{3}{a}^{3}$) |
5.某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.[毛利润=(售价-进价)×销售量]
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
| A | B | |
| 进价(万元/套) | 1.5 | 1.2 |
| 售价(万元/套) | 1.65 | 1.4 |
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
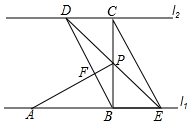 如图,直线l1∥l2,线段AB在l1上,BC⊥l1交l2于点C,且AB=BC=2cm,点P在点B、C之间,过点P的直线分别交l2、l1于点D、E;已知∠CDP=45°.
如图,直线l1∥l2,线段AB在l1上,BC⊥l1交l2于点C,且AB=BC=2cm,点P在点B、C之间,过点P的直线分别交l2、l1于点D、E;已知∠CDP=45°. 如图,按要求作图:
如图,按要求作图: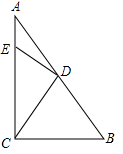 我们定义:有一组对角相等而另一组对角不相等的四边形叫做“等对角四边形”
我们定义:有一组对角相等而另一组对角不相等的四边形叫做“等对角四边形”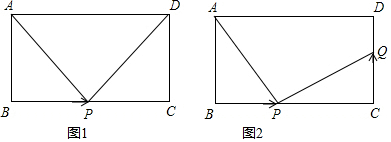
 如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线BE交AD于点E,则DE=3.
如图,在?ABCD中,AB=4,BC=7,∠ABC的平分线BE交AD于点E,则DE=3.