��Ŀ����
18��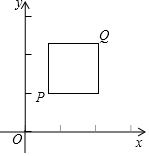 ��ƽ��ֱ������ϵxOy�У���P������Ϊ��x1��y1������Q������Ϊ��x2��y2������x1��x2��y1��y2����P��QΪij�����ε��������㣬�Ҹ������εı߾���ij��������ƽ�У����غϣ������P��Q��Ϊ�������ε㡱������P�ǵ�Q�ġ������ε㡱����QҲ�ǵ�P�ġ������ε㡱������ͼ�ǵ�P��Q��Ϊ�������ε㡱��ʾ��ͼ��
��ƽ��ֱ������ϵxOy�У���P������Ϊ��x1��y1������Q������Ϊ��x2��y2������x1��x2��y1��y2����P��QΪij�����ε��������㣬�Ҹ������εı߾���ij��������ƽ�У����غϣ������P��Q��Ϊ�������ε㡱������P�ǵ�Q�ġ������ε㡱����QҲ�ǵ�P�ġ������ε㡱������ͼ�ǵ�P��Q��Ϊ�������ε㡱��ʾ��ͼ����1����֪��A�������ǣ�2��3�������������У����A��Ϊ�������ε㡱�������Ǣ٢ۣ�������ţ�
�٣�1��2�����ڣ�-1��5�����ۣ�3��2����
��2������B��1��2���ġ������ε㡱C��y���ϣ���ֱ��BC�ı���ʽ��
��3����D������Ϊ��-1��0������M������Ϊ��2��m������N���߶�OD��һ���㣨���˵㣩������M��N��Ϊ�������ε㡱����m��ȡֵ��Χ��
���� ��1�����������ε����ʿɵó�|x1-x2|=|y1-y2|�����բ٢ڢ۵����꼴�ɵó����ۣ�
��2���ɵ�B�������ϻ�Ϊ�������ε㡱���������������ɵó���C�����꣬�����ô���ϵ�����������ֱ��BC�ı���ʽ��
��3������O��D�ֱ�����x��н�Ϊ45���ֱ�ߣ��ҳ���O��D��Ӧ�ġ������ε㡱�����꣬�ɴ˼��ɵó����ۣ�
��� �⣺��1���ߵ�P��x1��y1������Q��x2��y2����Ϊ�������ε㡱��
��|x1-x2|=|y1-y2|��
��|2-1|=|3-2|��|-1-2|��|5-3|��|3-2|=|2-3|��
�����A��Ϊ�������ε㡱�������Ǣ٣�1��2�����ۣ�3��2����
�ʴ�Ϊ���٢ۣ�
��2���ߵ�B��1��2���ġ������ε㡱C��y���ϣ�
���C��������0��1������0��3����
��ֱ��BC�ı���ʽΪy=kx+b��
����B��C���������y=kx+b��
$\left\{\begin{array}{l}{b=1}\\{k+b=2}\end{array}\right.$��$\left\{\begin{array}{l}{b=3}\\{k+b=2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$��$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
��ֱ��BC�ı���ʽΪy=x+1��y=-x+3��
��3������O��D�ֱ�����x��н�Ϊ45���ֱ�ߣ���ͼ��ʾ��
�ߵ�M������Ϊ��2��m������N���߶�OD��һ���㣨���˵㣩����M��N��Ϊ�������ε㡱��
���D�������ε������ǣ�2��3������2��-3������O�������ε������ǣ�2��2������2��-2����
��2��m��3��-3��m��-2��
���� ���⿼��������ֱ���ཻ��ƽ�����⡢�����ε������Լ�����ϵ������һ�κ�������ʽ������Ĺؼ��ǣ���1�����������ε������ҳ�|x1-x2|=|y1-y2|����2�����ݵ�B�������ҳ���C�����ꣻ��3���ֱ��ҳ���O��D�������ε����꣮

| A�� | ���ӻ����ڲ���ŷ�ޱ� | |
| B�� | ���⻭һ�������Σ����ڽǺ�Ϊ360�� | |
| C�� | ��һö�ʵؾ��ȵ����ӣ������ĵ���Ϊ8 | |
| D�� | ƽ����ͬһ��ֱ�ߵ�����ֱ��ƽ�� |
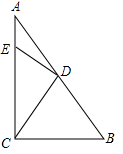 ���Ƕ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ�
���Ƕ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ�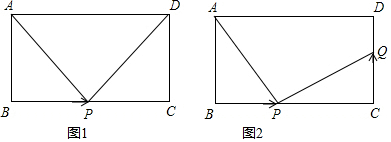

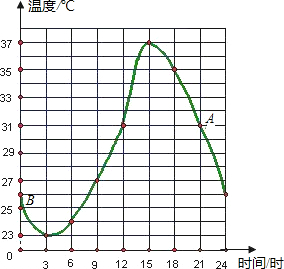 ��ͼ��ij��ij���¶ȱ仯�����������ͼ��ش����⣺
��ͼ��ij��ij���¶ȱ仯�����������ͼ��ش����⣺ ��ͼ����?ABCD�У�AB=4��BC=7����ABC��ƽ����BE��AD�ڵ�E����DE=3��
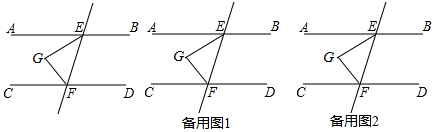
��ͼ����?ABCD�У�AB=4��BC=7����ABC��ƽ����BE��AD�ڵ�E����DE=3��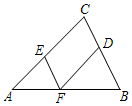 ��ͼ����D��E��F�ֱ���������ABC�ı�BC��CA��AB�ϵĵ㣬DF��CA����EFD=��C��
��ͼ����D��E��F�ֱ���������ABC�ı�BC��CA��AB�ϵĵ㣬DF��CA����EFD=��C��